
某高校在2011年的自主招生考试成绩
中随机抽取100名学生的笔试成绩,按成绩
分组:第1组[75,80),第2组[80,85),
第3组[85,90),第4组[90,95),第5组
[95,100]得到的频率分布直方图如图所示.
(Ⅰ)分别求第3,4,5组的频率;
(Ⅱ)若该校决定在笔试成绩高的第3,4,5组
中用分层抽样抽取6名学生进入第二轮面
试,求第3,4,5组每组各抽取多少名学生进入第二轮面试?
(Ⅲ)在(Ⅱ)的前提下,学校决定在这6名学生中随机抽取2名学生接受甲考官的面试,求第4组至少有一名学生被甲考官面试的概率.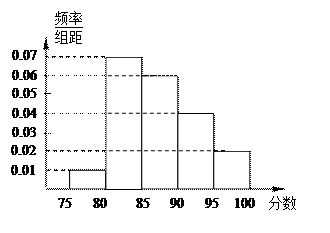
科目:高中数学 来源: 题型:解答题
(本题满分12分)
今年十一黄金周,记者通过随机询问某景区110名游客对景区的服务是否满意,得到如下的列联表:
性别与对景区的服务是否满意 单位:名
| | 男 | 女 | 总计 |
| 满意 | 50 | 30 | 80 |
| 不满意 | 10 | 20 | 30 |
| 总计 | 60 | 50 | 110 |
P(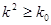 ) ) | 0.05 | 0.025 | 0.010 | 0.005 |
 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)某中学生物兴趣小组在学校生物园地种植了一批名贵树苗,为了解树苗的生长情况,从这批树苗中随机地测量了其中50棵树苗的高度(单位:厘米),并把这些高度列成了如下的频数分布表:
(1)在这批树苗中任取,其高度在85厘米以上的大约有多少棵;
(2)这批树苗的平均 高度大约是多少?(计算时可以用组中值代替各组数据的平均值);
高度大约是多少?(计算时可以用组中值代替各组数据的平均值);
(3)为了进一步获得研究资料,若从 组中移出一棵树苗,从
组中移出一棵树苗,从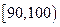 组中移出两棵树苗进行试验研究,则
组中移出两棵树苗进行试验研究,则 组中的树苗A和
组中的树苗A和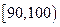 组中的树苗C同时被移出的概率是多少?
组中的树苗C同时被移出的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人。女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动。
(1)根据以上数据建立一个2×2列联表;
(2)判断休闲方式与性别是否有关。
(参考公式: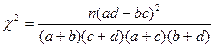
参考数据: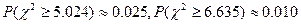 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了了解初三学生女生身高情况,某中学对初三女生身高进行了一次测量,所得数据整理后列出了频率分布表如下:
| 组别 | 频数 | 频率 |
| 145.5~149.5 | 1 | 0.02 |
| 149.5~153.5 | 4 | 0.08 |
| 153.5~157.5 | 20 | 0.40 |
| 157.5~161.5 | 15 | 0.30 |
| 161.5~165.5 | 8 | 0.16 |
| 165.5~169.5 | m | n |
| 合 计 | M | N |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某企业的某种产品产量与单位成本统计数据如下:
| 月份 | 1 | 2 | 3 | 4 | 5 | 6 |
| 产量(千克) | 2 | 3 | 4 | 3 | 4 | 5 |
| 单位成本(元/件) | 73 | 72 | 71 | 73 | 69 | 68 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
本小题满分12分)
为调查某市学生百米运动成绩,从该市学生中按照男女生比例随机抽取50名学生进行百米测试,学生成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组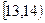 ,第二组
,第二组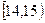 ……第五组
……第五组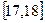 ,如图是按上述分组方法得到的频率分布直方图.
,如图是按上述分组方法得到的频率分布直方图.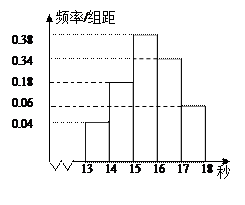
(Ⅰ)求这组数据的众数和中位数(精确到0.1);
(II)设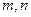 表示样本中两个学生的百米测
表示样本中两个学生的百米测
试成绩,已知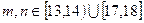
求事件“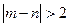 ”的概率.
”的概率.
(Ⅲ) 根据有关规定,成绩小于16秒为达标.
如果男女生使用相同的达标标准,则男女生达标情况如下 表
表
| 性别 是否达标 | 男 | 女 | 合计 |
| 达标 | 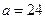 | 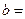 ______ ______ | _____ |
| 不达标 | 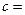 _____ _____ | 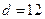 | _____ |
| 合计 | ______ | ______ | 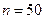 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小 题满分12分)
题满分12分)
上海世 博会深圳馆1号作品《大芬丽莎》是由大芬村507名画师集体创作的999幅
博会深圳馆1号作品《大芬丽莎》是由大芬村507名画师集体创作的999幅
油画组合而成的世界名画《蒙娜丽莎》,因其诞生于大芬村,因此被命名为《大芬丽莎》.某部门从参加创作的507名画师中随机抽出100名画师,测得画师年龄情况如下表所示.
| 分 组 (单位:岁) | 频数 | 频 率 |
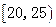 | 5 | 0.050 |
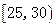 | ① | 0.200 |
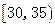 | 35 | ② |
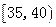 | 30 | 0.300 |
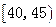 | 10 | 0.100 |
| 合 计 | 100 | 1.00 |
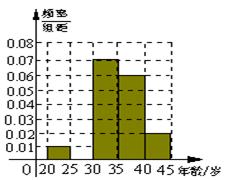
 在
在 岁的人数(结果取整数);
岁的人数(结果取整数); 深
深 画师担任解说员工作,记这2名画师中“年龄低于30岁”的人数为
画师担任解说员工作,记这2名画师中“年龄低于30岁”的人数为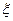 ,求
,求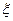 的分布列及数学期望.
的分布列及数学期望.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)
为考察某种甲型H1N1疫苗的效果,进行动物实验,得到如下疫苗效果的实验列联表:
| | 感染 |  未感染 未感染 | 总计 |
| 没服用 | 20 | 30 | 50 |
| 服用 | x | y | 50 |
| 总计 | M | N | 100 |
 从服从过疫苗的动物中任取两只,感染数为
从服从过疫苗的动物中任取两只,感染数为 工作人员曾计算过
工作人员曾计算过
 (
( 1)求出列联表中数据
1)求出列联表中数据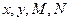 的值;
的值; 的均值(不要求计算过程),并比较大小,请解释所得出的结论的实际意义;
的均值(不要求计算过程),并比较大小,请解释所得出的结论的实际意义;
 参考数据:
参考数据: | 0.05 | 0.025 | 0.010 |
 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com