
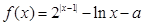 恰有两个不同的零点,则
恰有两个不同的零点,则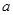 的取值范围是( )
的取值范围是( )A.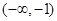 | B.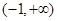 | C.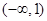 | D.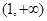 |



科目:高中数学 来源:不详 题型:解答题
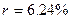 ,2000年该奖发放后基金总额约为21000万元。用
,2000年该奖发放后基金总额约为21000万元。用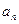
 表示为第
表示为第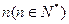 年该奖发放后的基金总额(2000年为第一年)。
年该奖发放后的基金总额(2000年为第一年)。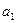 表示
表示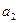 与
与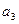 ,并根据所求结果归纳出
,并根据所求结果归纳出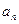 的表达式;
的表达式;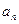 的表达式判断2011年度该奖各项奖金是否超过150万元?并计算从2001年到2011年该奖金累计发放的总额。
的表达式判断2011年度该奖各项奖金是否超过150万元?并计算从2001年到2011年该奖金累计发放的总额。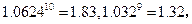
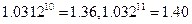 )
)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 )
)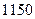 元,购买当天先付
元,购买当天先付
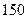 元,以后每月这一天都交付
元,以后每月这一天都交付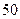 元,并加付欠款利息,月利率为
元,并加付欠款利息,月利率为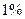 .若交付
.若交付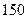 元后的第一个月开始算分期付款的第一个月,全部欠款付清后,请问买这件家电实际付款多少元?
元后的第一个月开始算分期付款的第一个月,全部欠款付清后,请问买这件家电实际付款多少元?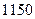 元,购买当天先付
元,购买当天先付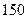 元,以后每月这一天还款一次,每次还款数额相同,
元,以后每月这一天还款一次,每次还款数额相同,
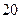 个月还清,月利率为
个月还清,月利率为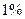 ,按复利计息.若交付
,按复利计息.若交付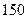 元后的第一个月开始算分期付款的第一个月,全部欠款付清后,请问买这件家电实际付款多少元?每月还款多少元?(最后结果保留4个有
元后的第一个月开始算分期付款的第一个月,全部欠款付清后,请问买这件家电实际付款多少元?每月还款多少元?(最后结果保留4个有 效数字)
效数字)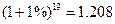 ,
,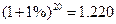 ,
,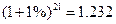 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 在定义域内是增函数;③函数
在定义域内是增函数;③函数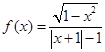 图象关于原点对称;④既是奇函数又是偶函数的函数一定是
图象关于原点对称;④既是奇函数又是偶函数的函数一定是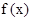 ="0"
="0" 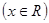 ; ⑤函数y=f(x+2)图象与函数y=f(2-x)图象关于直线x=2对称;其中正确命题的个数为:( )
; ⑤函数y=f(x+2)图象与函数y=f(2-x)图象关于直线x=2对称;其中正确命题的个数为:( )| A.0个 | B.1个 | C.2个 | D.3个 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com