
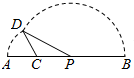
 如图,线段AB=16,点C在线段AB上,且AC=6,P为段CB上一动点,点A绕点C旋转后与点B绕点P旋转后重合于点D.则△CPD面积的最大值为( )
如图,线段AB=16,点C在线段AB上,且AC=6,P为段CB上一动点,点A绕点C旋转后与点B绕点P旋转后重合于点D.则△CPD面积的最大值为( )| A. | 9 | B. | 12 | C. | 15 | D. | 20 |
分析 本题要根据实际情况计算出面积函数的定义域,可以看出所给的条件是△CPD,故可根据其是三角形求出自变量的范围.面积表达式可以用海伦公式求出,对所得的函数运用基本不等式,可求出函数的最大值.
解答 解:由题意,DC=6,CP=x,DP=10-x,
由△CPD的三边的关系,可得$\left\{\begin{array}{l}{6+x>10-x}\\{x+10-x>6}\\{6+10-x>x}\end{array}\right.$,解得x∈(2,8)
如图,三角形的周长是一个定值16,
故其面积可用海伦公式S△CPD=$\sqrt{s(s-a)(s-b)(s-c)}$,
其中s=$\frac{1}{2}$(a+b+c),
即△CPD的面积为$\sqrt{8•(8-6)•(8-x)•(8-10+x)}$
=$\sqrt{16(8-x)(x-2)}$,
由(8-x)(x-2)≤($\frac{8-x+x-2}{2}$)2=9,
当且仅当8-x=x-2,可得x=5,取得最大值.
即有△CPD的面积最大值为12.
故选为:B.
点评 本题考查根据实际问题选择函数类型,本题中求面积用到了海伦公式,学习中积累一些知识储备,视野开阔,易找出简单的解题方法.本题考查到了基本不等式的运用,有一定的综合性.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | y=x${\;}^{\frac{1}{2}}$ | B. | y=2x | C. | y=x3 | D. | y=log2x |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 6 | C. | -3 | D. | -6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-3,0] | B. | (-∞,-3]∪[0,+∞) | C. | [0,3] | D. | (-∞,0]∪[3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x=y,则x2=y2”的逆否命题为真命题 | |
| B. | “x=-1”是“x2-5x-6=0”的必要不充分条件 | |
| C. | 命题“若x2=1,则x=1”的否命题为:“若x2=1,则x≠1” | |
| D. | 命题“?x∈R使得x2+x+1<0”的否定是:“?x∈R均有x2+x+1<0” |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 f′(x0) | B. | $\frac{1}{2}$ f′(x0) | C. | f′(x0) | D. | 4 f′(x0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com