
| A. | 2 f′(x0) | B. | $\frac{1}{2}$ f′(x0) | C. | f′(x0) | D. | 4 f′(x0) |
分析 根据题意,把题目中的算式变形,再利用导数的概念即可得出答案.
解答 解:∵f(x)在x=x0处的导数存在,
∴当h→0时 $\frac{f({x}_{0}+h)-f({x}_{0}-h)}{2h}$=$\underset{lim}{h→0}$$\frac{[f{(x}_{0}+h)-f{(x}_{0})]+[f{(x}_{0})-f{(x}_{0}-h)]}{2h}$
=$\frac{1}{2}$$\underset{lim}{h→0}$$\frac{f{(x}_{0}+h)}{h}$+$\frac{1}{2}$$\underset{lim}{h→0}$$\frac{f{(x}_{0})-f{(x}_{0}-h)}{h}$
=$\frac{1}{2}$f′(x0)+$\frac{1}{2}$f′(x0)
=f′(x0).
故选:C.
点评 本题考查了导数的概念与应用问题,是基础题目.


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
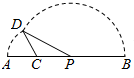 如图,线段AB=16,点C在线段AB上,且AC=6,P为段CB上一动点,点A绕点C旋转后与点B绕点P旋转后重合于点D.则△CPD面积的最大值为( )
如图,线段AB=16,点C在线段AB上,且AC=6,P为段CB上一动点,点A绕点C旋转后与点B绕点P旋转后重合于点D.则△CPD面积的最大值为( )| A. | 9 | B. | 12 | C. | 15 | D. | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 11 | B. | 27 | C. | 31 | D. | 35 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y={log_{\frac{1}{2}}}x$ | B. | $y={({\frac{1}{2}})^x}$ | C. | y=log2x | D. | y=2-x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | i | D. | -i |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com