
【题目】由直线![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 组成的图形中,共有同旁内角______对.
组成的图形中,共有同旁内角______对.
【答案】82
【解析】
首先指出,在“三线八角”基本图形中,一个“三线八角”图形与其截线上的一条线段构成一一对应,
而一个基本图形上有2对同旁内角,因而,计算同旁内角可转化为计算截线上的线段条数来解决,
问题只是,出现多重交点时,讨论要细致一些.
作出所给直线的图象(如图),先计算图中的基本图形个数.

(1)以直线![]() 为截线.
为截线.
由图可见,此截线与4条直线相交得4个交点,
从这4个交点中取出两个作截点(相当于两条直线被![]() 所截),
所截),
对应着一个基本图形,共得基本图形![]() (个).
(个).
(2)以直线![]() 为截线,
为截线,
由图可见,此截线与4条直线相交有4个交点,同理可得基本图形![]() (个).
(个).
(3)以直线![]() 为截线,
为截线,
由图可见,此截线与5条直线相交有5个交点,同理可得基本图形![]() (个).
(个).
(4)以![]() 为截线,
为截线,
由图可见,此截线与5条直线相交于4个交点,其中原点为二重交点,
在计算基本图形时要计算两次,
考虑更一般的情况,设截线![]() 与若干条直线相交于
与若干条直线相交于![]() 、
、![]() 、
、![]() 、
、![]() ,其中
,其中![]() 点上
点上![]() 与
与![]() 条直线相交,如图所示.
条直线相交,如图所示.

1)当取![]() 为第一个截点时,第二个截点可取
为第一个截点时,第二个截点可取![]() 、
、![]() 、
、![]() 之一,
之一,
对应基本图形有![]() (个).①
(个).①
2)当取![]() 为第一个截点时,第二个截点可取
为第一个截点时,第二个截点可取![]() 、
、![]() 之一,
之一,
对应基本图形有![]() (个). ②
(个). ②
3)当取![]() 为第一个截点时,第二个截点可取
为第一个截点时,第二个截点可取![]() ,
,
对应基本图形有![]() (个).③
(个).③
![]() 可得以
可得以![]() 为截线的基本图形,
为截线的基本图形,
有![]() (个).④
(个).④
取![]() ,
,![]() ,可得以
,可得以![]() 为截线的基本图形,
为截线的基本图形,
有![]() (个).
(个).
(5)以![]() 为截线.
为截线.
在式④中取![]() ,
,![]() ,得
,得![]() (个).
(个).
(6)以![]() 为截线.
为截线.
在式④中取![]() ,
,![]() ,得
,得![]() (个).
(个).
相加得![]() .
.
故同旁内角共有82对.


 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源: 题型:
【题目】对于定义城为R的函数![]() ,若满足:①
,若满足:①![]() ;②当
;②当![]() ,且
,且![]() 时,都有
时,都有![]() ;③当
;③当![]() 且
且![]() 时,都有
时,都有![]() ,则称
,则称![]() 为“偏对称函数”.下列函数是“偏对称函数”的是( )
为“偏对称函数”.下列函数是“偏对称函数”的是( )
A.![]() B.
B.![]()
C.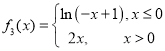 D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
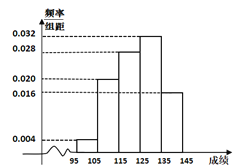
【题目】半期考试后,班长小王统计了50名同学的数学成绩,绘制频率分布直方图如图所示.
![]() 根据频率分布直方图,估计这50名同学的数学平均成绩;
根据频率分布直方图,估计这50名同学的数学平均成绩;
![]() 用分层抽样的方法从成绩低于115的同学中抽取6名,再在抽取的这6名同学中任选2名,求这两名同学数学成绩均在
用分层抽样的方法从成绩低于115的同学中抽取6名,再在抽取的这6名同学中任选2名,求这两名同学数学成绩均在![]() 中的概率.
中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的右焦点为F,点A(一2,2)为椭圆C内一点。若椭圆C上存在一点P,使得|PA|+|PF|=8,则m的取值范围是( ).
的右焦点为F,点A(一2,2)为椭圆C内一点。若椭圆C上存在一点P,使得|PA|+|PF|=8,则m的取值范围是( ).
A. ![]() B. [9,25] C.
B. [9,25] C. ![]() D. [3,5]
D. [3,5]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知椭圆C:![]() 的左右焦点分别为F1,F2,直线l:y=kx+m与椭圆C交于A,B两点.O为坐标原点.
的左右焦点分别为F1,F2,直线l:y=kx+m与椭圆C交于A,B两点.O为坐标原点.
(1)若直线l过点F1,且|AB|=![]() ,求k的值;
,求k的值;
(2)若以AB为直径的圆过原点O,试探究点O到直线AB的距离是否为定值?若是,求出该定值;若不是,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解甲、乙两个工厂生产的轮胎的宽度是否达标,分别从两厂随机各选取了![]() 个轮胎,将每个轮胎的宽度(单位:
个轮胎,将每个轮胎的宽度(单位: ![]() )记录下来并绘制出如下的折线图:
)记录下来并绘制出如下的折线图:
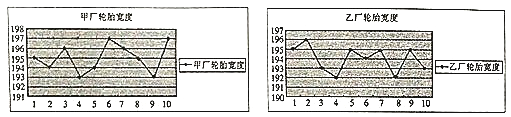
(1)分别计算甲、乙两厂提供的![]() 个轮胎宽度的平均值;
个轮胎宽度的平均值;
(2)轮胎的宽度在![]() 内,则称这个轮胎是标准轮胎.
内,则称这个轮胎是标准轮胎.
(i)若从甲乙提供的![]() 个轮胎中随机选取
个轮胎中随机选取![]() 个,求所选的轮胎是标准轮胎的概率
个,求所选的轮胎是标准轮胎的概率![]() ;
;
(ii)试比较甲、乙两厂分别提供的![]() 个轮胎中所有标准轮胎宽度的方差大小,根据两厂的标准轮胎宽度的平均水平及其波动情况,判断这两个工厂哪个厂的轮胎相对更好?
个轮胎中所有标准轮胎宽度的方差大小,根据两厂的标准轮胎宽度的平均水平及其波动情况,判断这两个工厂哪个厂的轮胎相对更好?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com