[题目]在三棱锥各棱所在的6条直线上.互相垂直的最多有儿对? 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】在三棱锥各棱所在的6条直线上，互相垂直的最多有儿对？（每两条组成一对）

【答案】6

【解析】

分三步证明最多有6对互相垂直的直线.

（1）6对是可以达到的.

当且时，由线面垂直的性质有，，.

又由三垂线定理，有，.这就得出6对互相垂直的直线(如图所示).

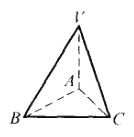
(2)8对是不可能的.

由于一个三角形的内角中最多有一个直角，最少有两个锐角，所以4个面三角形至少有8个锐角，又由6条直线可以组成对直线，知，互相垂直的直线不超过7对.

(3)7对是不可能的.

若不然，有7对垂直直线，因异面直线只有3对，故至少有4对垂直直线是共面的，

得三棱锥的4个表面都必须是直角三角形（得4对）.

进而3对成异面直线的棱也互相垂直.

此时，三棱锥的一个顶点在所对面上的射影必是该三角形的垂心，

而直角三角形的垂心就是直角顶点，所以这个三棱锥的一条侧棱与底面垂直，且垂足就是垂面三角形的顶点(图中，).

这时底面三角形直角顶点的对面为锐角三角形（为锐角三角形），与4个面均为直角三角形矛盾.

综上得，互相垂直的直线最多有6对.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】某造船公司年造船量是20艘,已知造船艘的产值函数为 (单位:万元),成本函数为(单位:万元),又在经济学中,函数的边际函数定义为.

(1)求利润函数及边际利润函数.(提示:利润=产值-成本)

(2)问年造船量安排多少艘时,可使公司造船的年利润最大?

(3)求边际利润函数的单调递减区间,并说明单调递减在本题中的实际意义是什么?

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】对于两个定义域相同的函数、，若存在实数，，使则称函数是由“基函数”生成的.

（1）若和生成一个偶函数，求的值；

（2）若是由和生成，其中，.且求的取值范围；

（3）利用“基函数，”生成一个函数，使得满足：

①是偶函数，②有最小值，求的解析式.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】△ABC的内角A. B. C的对边分别为a，b，c，己知＝b（c－asinC）。

（1)求角A的大小；

(2）若b＋c＝，，求△ABC的面积。

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】由直线，，，，，组成的图形中，共有同旁内角______对.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某校为了增强学生的记忆力和辨识力，组织了一场类似《最强大脑》的PK赛，两队各由4名选手组成，每局两队各派一名选手PK，比赛四局.除第三局胜者得2分外，其余各局胜者均得1分，每局的负者得0分.假设每局比赛A队选手获胜的概率均为，且各局比赛结果相互独立，比赛结束时A队的得分高于B队的得分的概率为( )