
【题目】已知函数![]() 求:
求:
(1)![]() 的单调区间
的单调区间
(2)![]() 的单调区间在[0,3]上的最大值与最小值.
的单调区间在[0,3]上的最大值与最小值.
【答案】(1)增区间为![]() 和
和![]() ,减区间为
,减区间为![]() ;(2)最大值为4,最小值为
;(2)最大值为4,最小值为![]()
【解析】
(1)求出导函数![]() ,由
,由![]() 确定增区间,由
确定增区间,由![]() 确定减区间;
确定减区间;
(2)由(1)可得函数在![]() 上的单调性、极值,可列表,确定出最值.
上的单调性、极值,可列表,确定出最值.
(1)f′(x)=x2-4=(x+2)(x-2),
令f′(x)>0 得x<-2 或 x>2
令f′(x)<0 得-2<x<2
所以函数f(x)=![]() x3-4x+4的单调递增区间为
x3-4x+4的单调递增区间为![]() 和
和![]()
所以函数f(x)=![]() x3-4x+4的单调递减区间为
x3-4x+4的单调递减区间为![]()
(2)f′(x)=x2-4=(x+2)(x-2),
令f′(x)=0,解得x1=-2(舍去),x2=2.
当x变化时,f′(x),f(x)的变化情况如下表:
x | 0 | (0,2) | 2 | (2,3) | 3 |
f′(x) | - | 0 | + | ||
f(x) | 4 | 单调递减 | 极小值 | 单调递增 | 1 |
∴函数f(x)=![]() x3-4x+4在[0,3]上最大值为4,最小值为
x3-4x+4在[0,3]上最大值为4,最小值为![]() .
.


科目:高中数学 来源: 题型:
【题目】为了解某班学生喜好体育运动是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
喜好体育运动 | 不喜好体育运动 | |
男生 | 5 | |
女生 | 10 |
已知按喜好体育运动与否,采用分层抽样法抽取容量为10的样本,则抽到喜好体育运动的人数为6.
(1)请将上面的列联表补充完整;
(2)能否在犯错概率不超过0.01的前提下认为喜好体育运动与性别有关?说明你的理由;
(3)在上述喜好体育运动的6人中随机抽取两人,求恰好抽到一男一女的概率.
参考公式:![]() .
.
独立性检验临界值表:
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子里装有9个球,其中有4个红球,3个黄球和2个绿球,这些球除颜色外完全相同
![]() 从盒子中随机取出2个球,求取出的2个球颜色相同的概率.
从盒子中随机取出2个球,求取出的2个球颜色相同的概率.
![]() 从盒子中随机取出4个球,其中红球个数分别记为X,求随机变量X的分布列和数学期望.
从盒子中随机取出4个球,其中红球个数分别记为X,求随机变量X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位同学参加诗词大赛,各答3道题,每人答对每道题的概率均为![]() ,且各人是否答对每道题互不影响.
,且各人是否答对每道题互不影响.
(Ⅰ)用![]() 表示甲同学答对题目的个数,求随机变量
表示甲同学答对题目的个数,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅱ)设![]() 为事件“甲比乙答对题目数恰好多2”,求事件
为事件“甲比乙答对题目数恰好多2”,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
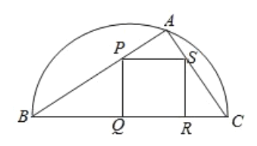
【题目】如图,某园林单位准备绿化一块直径为BC的半圆形空地,![]() 外的地方种草,
外的地方种草,![]() 的内接正方形PQRS为一水池,其余的地方种花.若
的内接正方形PQRS为一水池,其余的地方种花.若![]() ,
,![]() ,设
,设![]() 的面积为
的面积为![]() ,正方形PQRS的面积为
,正方形PQRS的面积为![]() .
.
(1)用a,![]() 表示
表示![]() 和
和![]() ;
;
(2)当a为定值,![]() 变化时,求
变化时,求![]() 的最小值,及此时的
的最小值,及此时的![]() 值.
值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位选派甲乙丙三人组队参加知识竞赛,甲乙丙三人在同时回答一道问题时,已知甲答对的概率是![]() ,甲丙两人都答错的概率是
,甲丙两人都答错的概率是![]() ,乙丙两人都答对的概率是
,乙丙两人都答对的概率是![]() ,规定每队只要有一人答对此题则该队答对此题.
,规定每队只要有一人答对此题则该队答对此题.
(1)求该单位代表队答对此题的概率;
(2)此次竞赛规定每队都要回答10道必答题,每道题答对得20分,答错得![]() 分.若该单位代表队答对每道题的概率相等且回答任一道题的对错对回答其他题没有影响,求该单位代表队必答题得分的均值(精确到1分).
分.若该单位代表队答对每道题的概率相等且回答任一道题的对错对回答其他题没有影响,求该单位代表队必答题得分的均值(精确到1分).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com