
【题目】某造船公司年造船量是20艘,已知造船![]() 艘的产值函数为
艘的产值函数为![]() (单位:万元),成本函数为
(单位:万元),成本函数为![]() (单位:万元),又在经济学中,函数
(单位:万元),又在经济学中,函数![]() 的边际函数
的边际函数![]() 定义为
定义为![]() .
.
(1)求利润函数![]() 及边际利润函数
及边际利润函数![]() .(提示:利润=产值-成本)
.(提示:利润=产值-成本)
(2)问年造船量安排多少艘时,可使公司造船的年利润最大?
(3)求边际利润函数![]() 的单调递减区间,并说明单调递减在本题中的实际意义是什么?
的单调递减区间,并说明单调递减在本题中的实际意义是什么?
【答案】(1)![]() 且
且![]() ;(2)12;(3)
;(2)12;(3)![]() 且
且![]() .
.
【解析】
(1)先根据利润=产值-成本求P(x),再求边际利润函数![]() .(2)利用导数求年造船量安排多少艘时,可使公司造船的年利润最大.(3)利用二次函数求边际利润函数
.(2)利用导数求年造船量安排多少艘时,可使公司造船的年利润最大.(3)利用二次函数求边际利润函数![]() 的单调递减区间,并说明单调递减在本题中的实际意义.
的单调递减区间,并说明单调递减在本题中的实际意义.
(1)P(x)=R(x)-C(x)=-10x3+45x2+3240x-5(x∈N+,且1≤x≤20);
MP(x)=P(x+1)-P(x)=-30x2+60x+3275(x∈N+,且1≤x≤19).
(2)P'(x)=-30x2+90x+3240=-30(x-12)(x+9),
∵x>0,∴P'(x)=0时,x=12,
∴当0<x<12时,P'(x)>0,
当x>12时,P'(x)<0,∴x=12时,P(x)有最大值.
即年造船量安排12艘时,可使公司造船的年利润最大.
(3)MP(x)=-30x2+60x+3275=-30(x-1)2+3305.所以,当x≥1时,MP(x)是减函数,
所以单调减区间为[1,19],且x∈N+.
MP(x)是减函数的实际意义是:随着产量的增加,每艘船的利润与前一艘船的利润比较,利润在减少.


科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() (
(![]() )的上顶点为
)的上顶点为![]() ,圆
,圆![]() 经过点
经过点![]() .
.

(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作直线
作直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,过点
两点,过点![]() 作直线
作直线![]() 的垂线
的垂线![]() 交圆
交圆![]() 于另一点
于另一点![]() .若△PQN的面积为3,求直线
.若△PQN的面积为3,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() 是偶函数,求
是偶函数,求![]() 的值;
的值;
(2)设函数![]() ,当
,当![]() 时,
时,![]() 有且只有一个实数根,求
有且只有一个实数根,求![]() 的取值范围;
的取值范围;
(3)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有两个不相等的实数根
上有两个不相等的实数根![]() ,
,![]() ,证明:
,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在盒子里有大小相同,仅颜色不同的乒乓球共10个,其中红球5个,白球3个,蓝球2个.现从中任取出一球确定颜色后放回盒子里,再取下一个球.重复以上操作,最多取3次,过程中如果取出蓝色球则不再取球.
(1)求整个过程中恰好取到2个白球的概率;
(2)求取球次数的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义城为R的函数![]() ,若满足:①
,若满足:①![]() ;②当
;②当![]() ,且
,且![]() 时,都有
时,都有![]() ;③当
;③当![]() 且
且![]() 时,都有
时,都有![]() ,则称
,则称![]() 为“偏对称函数”.下列函数是“偏对称函数”的是( )
为“偏对称函数”.下列函数是“偏对称函数”的是( )
A.![]() B.
B.![]()
C.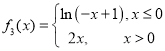 D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】上饶市在某次高三适应性考试中对数学成绩数据统计显示,全市10000名学生的成绩近似服从正态分布![]() ,现某校随机抽取了50名学生的数学成绩分析,结果这50名学生的成绩全部介于85分到145分之间,现将结果按如下方式分为6组,第一组
,现某校随机抽取了50名学生的数学成绩分析,结果这50名学生的成绩全部介于85分到145分之间,现将结果按如下方式分为6组,第一组![]() ,第二组
,第二组![]() ,…,第六组
,…,第六组![]() ,得到如图所示的频率分布直方图:
,得到如图所示的频率分布直方图:
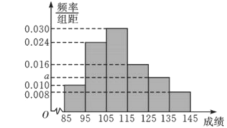
(1)试由样本频率分布直方图估计该校数学成绩的平均分数;
(2)若从这50名学生中成绩在125分(含125分)以上的同学中任意抽取3人,该3人在全市前13名的人数记为![]() ,求
,求![]() 的概率.
的概率.
附:若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com