
| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
分析 画出图形,在边OC上取点D,作DE⊥平面AOB,根据条件便知垂足E在∠AOB的平分线上,然后再过E作EF⊥OB,并连接DF,可设OD=x,这样根据所给的∠COB=θ,OC与平面AOB所成的角即可得到$\frac{\sqrt{3}}{3}xcos\frac{θ}{2}=x•cosθ$,进一步得到$\frac{\sqrt{3}}{3}cos\frac{θ}{2}=2co{s}^{2}\frac{θ}{2}-1$,这样解出cos$\frac{θ}{2}$,从而得到$\frac{θ}{2}$,进而得出θ值.
解答 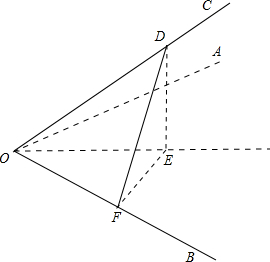 解:如图,
解:如图,
在边OC上取一点D,过D作DE⊥平面AOB,根据已知条件,垂足E在∠AOB的角平分线上,过E作EF⊥OB,垂足为F,连接DF,则:
∵DE⊥平面AOB,OB?平面AOB;
∴DE⊥OB,即OB⊥DE;
又OB⊥EF,DE∩EF=E;
∴OB⊥平面DEF;
∴OB⊥DF,设OD=x,则:OE=$\frac{\sqrt{3}}{3}x$;
∴$OF=\frac{\sqrt{3}}{3}x•cos\frac{θ}{2}=x•cosθ$;
∴$\frac{\sqrt{3}}{3}cos\frac{θ}{2}=cosθ$;
∴$\frac{\sqrt{3}}{3}cos\frac{θ}{2}=2co{s}^{2}\frac{θ}{2}-1$;
解得$cos\frac{θ}{2}=\frac{\sqrt{3}}{2}$,或$-\frac{\sqrt{3}}{3}$;
∵θ为锐角,∴$\frac{θ}{2}$为锐角;
∴$cos\frac{θ}{2}=\frac{\sqrt{3}}{2}$;
∴$\frac{θ}{2}=30°$;
∴θ=60°.
故选:C.
点评 考查线直线与平面所成角的概念,线面垂直的性质及判定定理,以及直角三角形的边角关系,二倍角的余弦公式.


 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:高中数学 来源: 题型:解答题
 如图所示,已知过抛物线x2=2py(p>0)的焦点F的直线l与抛物线相交于A,B两点
如图所示,已知过抛物线x2=2py(p>0)的焦点F的直线l与抛物线相交于A,B两点查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | |a|>1 | B. | |a||<$\sqrt{2}$ | C. | |a|>$\sqrt{2}$ | D. | 1<|a|<$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com