
分析 根据指数幂的运算性质计算即可.
解答 解:(1)(a${\;}^{\frac{2}{3}}$b${\;}^{\frac{1}{2}}$)(-3a${\;}^{\frac{1}{2}}$+b${\;}^{\frac{1}{3}}$)÷($\frac{1}{3}$a${\;}^{\frac{1}{6}}$b${\;}^{\frac{5}{6}}$)=-3×3${a}^{\frac{2}{3}+\frac{1}{2}-\frac{1}{6}}$${b}^{\frac{1}{2}+\frac{1}{3}-\frac{5}{6}}$=-9a,
(2)$\frac{\root{3}{{a}^{4}}-8\root{3}{a}•b}{\root{3}{{a}^{2}}+2\root{3}{ab}+4\root{3}{{b}^{2}}}$÷(1-2$\root{3}{\frac{b}{a}}$)×$\root{3}{a}$=$\root{3}{{a}^{\;}}$($\root{3}{a}$-2$\root{3}{b}$)÷(1-2$\root{3}{\frac{b}{a}}$)×$\root{3}{a}$=a(1-2$\root{3}{\frac{b}{a}}$)÷(1-2$\root{3}{\frac{b}{a}}$)=a
点评 本题考查指数幂的运算法则,培养了学生的计算能力,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | y=±2x | B. | y=±$\frac{1}{2}$x | C. | y=±$\sqrt{2}$x | D. | y=±$\frac{\sqrt{2}}{2}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2π | B. | $\frac{3π}{2}$ | C. | π | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源:2017届广西南宁二中等校高三8月联考数学(理)试卷(解析版) 题型:解答题
选修4-5:不等式选讲
已知函数 ,
, ;
;
(1)求不等式 的解集;
的解集;
(2)若对任意的 ,
, ,求
,求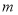 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2016-2017学年重庆市高二上学期入学考试数学试卷(解析版) 题型:解答题
已知 是函数
是函数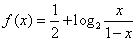 的图象上任意两点,且
的图象上任意两点,且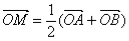 ,点
,点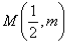 .
.
(I)求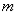 的值;
的值;
(II)若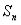 =
=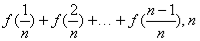 ∈N*,且n≥2,求
∈N*,且n≥2,求 .
.
(III)已知 =
= 其中
其中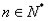 .
. 为数列{an}的前
为数列{an}的前 项和,若
项和,若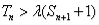 对一切
对一切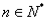 都成立,试求
都成立,试求 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com