练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知f(x)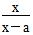＝(x≠a)．

    (1)若a＝－2，试证f(x)在(－∞，－2)内单调递增；

    (2)若a>0且f(x)在(1，＋∞)内单调递减，求a的取值范围．


    1)证明　任设x1<x2<－2，

    则f(x1)－f(x2)＝

    ∵(x1＋2)(x2＋2)>0，x1－x2<0，

    ∴f(x1)<f(x2)，

    ∴f(x)在(－∞，－2)内单调递增．

    (2)解　任设1<x1<x2，则

    f(x1)－f(x2)＝

    ∵a>0，x2－x1>0，

    ∴要使f(x1)－f(x2)>0，只需(x1－a)(x2－a)>0恒成立，

    ∴a≤1.

    综上所述知0<a≤1.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    若f(x)＝ 则函数g(x)＝f(x)－x的零点为____________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数f(x)＝＋m (a>1)恒过点(1,10)，则m＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)对一切x，y∈R，都有f(x＋y)＝f(x)＋f(y)．

    (1)求证：f(x)是奇函数；

    (2)若f(－3)＝a，用a表示f(12)．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设x1，x2为y＝f(x)的定义域内的任意两个变量，有以下几个命题：

    ①(x1－x2)[f(x1)－f(x2)]>0；②(x1－x2)[f(x1)－f(x2)]<0；

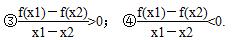    其中能推出函数y＝f(x)为增函数的命题为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝lg(x＋3)的定义域为M，g(x)＝的定义域为N，则M∩N＝__________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝若f(f(0))＝4a，则实数a＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    数列中，，且（，），则这个数列的通项公式               ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知集合A是集合Pn＝{1，2，3，…，n} (n≥3，n∈N*)的子集，且A中恰有3个元素，同时这3个元素的和是3的倍数．记符合上述条件的集合A的个数为f(n)．

    （1）求f(3)，f(4)；

    （2）求f(n)（用含n的式子表示）．

    查看答案和解析>>

    同步练习册答案