
【题目】已知下列命题:
①命题:x∈(0,2),3x>x3的否定是:x∈(0,2),3x≤x3;
②若f(x)=2x﹣2﹣x , 则x∈R,f(﹣x)=﹣f(x);
③若f(x)=x+ ![]() ,则x0∈(0,+∞),f(x0)=1;
,则x0∈(0,+∞),f(x0)=1;
④等差数列{an}的前n项和为Sn , 若a4=3,则S7=21;
⑤在△ABC中,若A>B,则sinA>sinB.
其中真命题是 . (只填写序号)
【答案】①②④⑤
【解析】解:对于①,命题:x∈(0,2),3x>x3的否定是:x∈(0,2),3x≤x3 , 正确;
对于②,若f(x)=2x﹣2﹣x , 则x∈R,f(﹣x)=﹣f(x),正确;
对于③,对于函数f(x)=x+ ![]() ,当且仅当x=0时,f(x)=1,故错;
,当且仅当x=0时,f(x)=1,故错;
对于④,等差数列{an}的前n项和为Sn , 若a4=3, ![]() ,故正确;
,故正确;
对于⑤,在△ABC中,若A>B,则a>b2RsinA>2RsinBsinA>sinB,故正确.
所以答案是:①②④⑤
【考点精析】掌握命题的真假判断与应用是解答本题的根本,需要知道两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系.


科目:高中数学 来源: 题型:
【题目】已知正项数列{an}的前n项和为Sn , 且 ![]() 是1与an的等差中项.
是1与an的等差中项.
(1)求数列{an}的通项公式;
(2)设Tn为数列{ ![]() }的前n项和,证明:
}的前n项和,证明: ![]() ≤Tn<1(n∈N*).
≤Tn<1(n∈N*).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】先把函数y=sin(x+φ)的图象上个点的横坐标缩短为原来的 ![]() (纵坐标不变),再向右平移
(纵坐标不变),再向右平移 ![]() 个单位,所得函数关于y轴对称,则φ的值可以是( )
个单位,所得函数关于y轴对称,则φ的值可以是( )
A.![]()
B.![]()
C.- ![]()
D.- ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
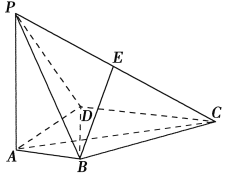
【题目】如图,在四棱锥![]() 中,
中,![]() ⊥底面
⊥底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 为棱
为棱![]() 的中点.
的中点.
(1)(理科生做)证明:![]() ;
;
(文科生做)证明:![]() ;
;
(2)(理科生做)若![]() 为棱
为棱![]() 上一点,满足
上一点,满足![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
(文科生做)求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数学家欧拉在1765年发现,任意三角形的外心、重心、垂心位于同一条直线上,这条直线称为欧拉线已知![]() 的顶点
的顶点![]() ,若其欧拉线的方程为
,若其欧拉线的方程为![]() ,则顶点
,则顶点![]() 的坐标为( )
的坐标为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (a>b>0)的上、下、左、右四个顶点分别为A,B,C,D,x轴正半轴上的点P满足|PA|=|PD|=2,|PC|=4。
(a>b>0)的上、下、左、右四个顶点分别为A,B,C,D,x轴正半轴上的点P满足|PA|=|PD|=2,|PC|=4。
(I)求椭圆C的标准方程以及点P的坐标;
(II)过点P作直线l交椭圆C于点M,N,是否存在这样的直线l使得△MNA和△MND的面积相等?若存在,请求出直线l的方程,若不存在,请说明理由;
(III)在(II)的条件下,求当直线l的倾斜角为钝角时△MND的面积。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
已知关于![]() 的不等式
的不等式![]() ,其中
,其中![]() .
.
(1)当![]() 变化时,试求不等式的解集
变化时,试求不等式的解集![]() ;
;
(2)对于不等式的解集![]() ,若满足
,若满足![]() (其中
(其中![]() 为整数集). 试探究集合
为整数集). 试探究集合![]() 能否为有限集?若 能,求出使得集合
能否为有限集?若 能,求出使得集合![]() 中元素个数最少的
中元素个数最少的![]() 的所有取值,并用列举法表示集合
的所有取值,并用列举法表示集合![]() ;若不能,请说明理由.
;若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥C﹣PAB中,AB⊥BC,PB⊥BC,PA=PB=5,AB=6,BC=4,点M是PC的中点,点N在线段AB上,且MN⊥AB. 
(1)求AN的长;
(2)求锐二面角P﹣NC﹣A的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com