
【题目】如图,在四棱锥![]() 中,
中,![]() ⊥底面
⊥底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 为棱
为棱![]() 的中点.
的中点.
(1)(理科生做)证明:![]() ;
;
(文科生做)证明:![]() ;
;
(2)(理科生做)若![]() 为棱
为棱![]() 上一点,满足
上一点,满足![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
(文科生做)求点![]() 到平面
到平面![]() 的距离.
的距离.
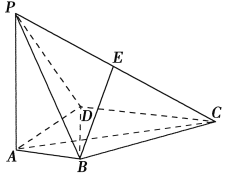
【答案】(1)见解析(2)理![]() ,文
,文![]()
【解析】
(1理)可通过以点![]() 为原点建立空间直角坐标系,然后确定
为原点建立空间直角坐标系,然后确定![]() 四点的坐标,最后通过求
四点的坐标,最后通过求![]() 得出
得出![]() ;
;
(1文)首先可证明四边形![]() 是平行四边形,再通过
是平行四边形,再通过![]() 证明
证明![]() 平面
平面![]() ;
;
(2理)先求出向量![]() ,然后求出平面
,然后求出平面![]() 和平面
和平面![]() 的法向量,最后求出二面角
的法向量,最后求出二面角![]() 的余弦值;
的余弦值;
(2文)可通过等面积法求出点![]() 到平面
到平面![]() 的距离。
的距离。
(1理)依题意,以点![]() 为原点建立空间直角坐标系(如图),
为原点建立空间直角坐标系(如图),
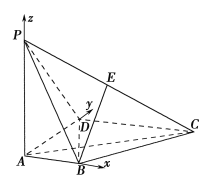 可得
可得![]() ,
,
![]() ,
,
由![]() 为棱
为棱![]() 的中点,
的中点,
得![]() ,
,
向量![]() ,
,![]() ,故
,故![]() ,
,
所以![]() .
.
(1文)取![]() 中点
中点![]() ,联接
,联接![]()
因为![]() 是
是![]() 中点,所以
中点,所以![]() 且
且![]()
所以![]() 且
且![]() ,四边形
,四边形![]() 是平行四边形
是平行四边形
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ;
;
(2理)向量![]() ,
,![]() ,
,![]() ,
,![]() .
.
由点![]() 在棱
在棱![]() 上,设
上,设![]() ,
,
故![]()
由![]() ,得
,得![]() ,因此
,因此![]() ,解得
,解得![]() ,
,
即![]() ,设
,设![]() 为平面
为平面![]() 的法向量,
的法向量,
则 ,即
,即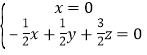 ,
,
不妨令![]() ,可得
,可得![]() 平面
平面![]() 的一个法向量.
的一个法向量.
取平面![]() 的法向量
的法向量![]() ,则
,则
![]() ,
,
易知,二面角![]() 是锐角,所以其余弦值为
是锐角,所以其余弦值为![]()
(2文)设![]() 到平面
到平面![]() 距离为
距离为![]() ,
,
![]()
在![]() 中,
中,![]() 因为
因为![]() ,
,![]()
所以![]() 平面
平面![]() ,
,
所以![]() ,在
,在![]() 中,
中,![]()
将数据代入得![]() 。
。


科目:高中数学 来源: 题型:
【题目】用6种颜色给右图四面体A﹣BCD的每条棱染色,要求每条棱只染一种颜色且共顶点的棱染不同的颜色,则不同的染色方法共有( )种. 
A.4080
B.3360
C.1920
D.720
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥![]() 中,
中, ![]() 面
面![]() ,
, ![]() 是平行四边形,
是平行四边形, ![]() ,
, ![]() ,点
,点![]() 为棱
为棱![]() 的中点,点
的中点,点![]() 在棱
在棱![]() 上,且
上,且![]() ,平面
,平面![]() 与
与![]() 交于点
交于点![]() ,则异面直线
,则异面直线![]() 与
与![]() 所成角的正切值为__________.
所成角的正切值为__________.
【答案】![]()
【解析】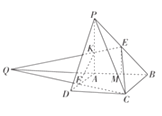
延长![]() 交
交![]() 的延长线与点Q,连接QE交PA于点K,设QA=x,
的延长线与点Q,连接QE交PA于点K,设QA=x,
由![]() ,得
,得![]() ,则
,则![]() ,所以
,所以![]() .
.
取![]() 的中点为M,连接EM,则
的中点为M,连接EM,则![]() ,
,
所以![]() ,则
,则![]() ,所以AK=
,所以AK=![]() .
.
由AD//BC,得异面直线![]() 与
与![]() 所成角即为
所成角即为![]() ,
,
则异面直线![]() 与
与![]() 所成角的正切值为
所成角的正切值为![]() .
.
【题型】填空题
【结束】
17
【题目】在极坐标系中,极点为![]() ,已知曲线
,已知曲线![]() :
: ![]() 与曲线
与曲线![]() :
: ![]() 交于不同的两点
交于不同的两点![]() ,
, ![]() .
.
(1)求![]() 的值;
的值;
(2)求过点![]() 且与直线
且与直线![]() 平行的直线
平行的直线![]() 的极坐标方程.
的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,点
,点![]() 满足
满足![]() ,记点
,记点![]() 的轨迹为
的轨迹为![]() .
.
(1)求轨迹![]() 的方程;
的方程;
(2)若直线![]() 过点
过点![]() 且与轨迹
且与轨迹![]() 交于
交于![]() 、
、![]() 两点.
两点.
(i)无论直线![]() 绕点
绕点![]() 怎样转动,在
怎样转动,在![]() 轴上总存在定点
轴上总存在定点![]() ,使
,使![]() 恒成立,求实数
恒成立,求实数![]() 的值.
的值.
(ii)在(i)的条件下,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知下列命题:
①命题:x∈(0,2),3x>x3的否定是:x∈(0,2),3x≤x3;
②若f(x)=2x﹣2﹣x , 则x∈R,f(﹣x)=﹣f(x);
③若f(x)=x+ ![]() ,则x0∈(0,+∞),f(x0)=1;
,则x0∈(0,+∞),f(x0)=1;
④等差数列{an}的前n项和为Sn , 若a4=3,则S7=21;
⑤在△ABC中,若A>B,则sinA>sinB.
其中真命题是 . (只填写序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
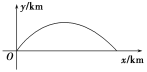
【题目】如图,建立平面直角坐标系,x轴在地平面上,y轴垂直于地平面,单位长度为1 km,某炮位于原点.已知炮弹发射后的轨迹在方程y=kx-![]() (1+k2)x2(k>0)表示的曲线上,其中k与发射方向有关.炮的射程是指炮弹落地点的横坐标.则炮的最大射程为( )
(1+k2)x2(k>0)表示的曲线上,其中k与发射方向有关.炮的射程是指炮弹落地点的横坐标.则炮的最大射程为( )
A. 20 km B. 10 km
C. 5 km D. 15 km
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一次函数f(x)=ax-2.
(1)当a=3时,解不等式|f(x)|<4;
(2)解关于x的不等式|f(x)|<4;
(3)若关于x的不等式|f(x)|≤3对任意x∈[0,1]恒成立,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com