
【题目】已知正项数列{an}的前n项和为Sn , 且 ![]() 是1与an的等差中项.
是1与an的等差中项.
(1)求数列{an}的通项公式;
(2)设Tn为数列{ ![]() }的前n项和,证明:
}的前n项和,证明: ![]() ≤Tn<1(n∈N*).
≤Tn<1(n∈N*).
【答案】
(1)解: n=1时,a1=1
n≥2时,由 ![]() 是1与an的等差中项,
是1与an的等差中项,
∴ ![]() ,
,
又 ![]() ,
,
两式相减得(an+an﹣1)(an﹣an﹣1﹣2)=0
∵an>0
∴an﹣an﹣1=2
∴{an}是以1为首项,2为公差的等差数列,即an=2n﹣1.
(2)解:∵ ![]() =
= ![]() =
= ![]()
∴Tn= ![]()
![]()
= ![]() .
.
∵n∈N+
∴Tn<1
又∵Tn递增.
∴ ![]() ,
,
综上, ![]() 成立
成立
【解析】(1)由等差中项,列出Sn与an的关系式,根据 ![]() 求解出数列{an}的通项公式.(2)数列{
求解出数列{an}的通项公式.(2)数列{ ![]() }的结构分析,采用裂项相消求数列前n项和Tn , 结合数列单调性及简单的放缩法,求得范围.
}的结构分析,采用裂项相消求数列前n项和Tn , 结合数列单调性及简单的放缩法,求得范围.
【考点精析】利用数列的前n项和和数列的通项公式对题目进行判断即可得到答案,需要熟知数列{an}的前n项和sn与通项an的关系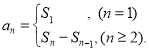 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.


科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,PA=PB=AB=BC=2,∠CBA=∠PBC=60°,Q为线段BC的中点.
(1)求证:PA⊥BC;
(2)求点Q到平面PAC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4―4:坐标系与参数方程]
在直角坐标系xOy中,曲线C的参数方程为![]() (θ为参数),直线l的参数方程为
(θ为参数),直线l的参数方程为![]() .
.
(1)若a=1,求C与l的交点坐标;
(2)若C上的点到l的距离的最大值为![]() ,求a.
,求a.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用6种颜色给右图四面体A﹣BCD的每条棱染色,要求每条棱只染一种颜色且共顶点的棱染不同的颜色,则不同的染色方法共有( )种. 
A.4080
B.3360
C.1920
D.720
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知抛物线的方程为x2=2py(p>0),过点A(0,﹣1)作直线l与抛物线相交于P,Q两点,点B的坐标为(0,1),连接BP,BQ,设QB,BP与x轴分别相交于M,N两点.如果QB的斜率与PB的斜率的乘积为﹣3,则∠MBN的大小等于 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ax2﹣a﹣lnx,其中a∈R.
(1)讨论f(x)的单调性;
(2)当x∈(1,+∞)时,xf(x)+xe1﹣x>1恒成立,求a的取值范围.(其中,e=2.718…为自然对数的底数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设F1,F2分别为双曲线![]() 的左、右焦点,A1,A2分别为这个双曲线的左、右顶点,P为双曲线右支上的任意一点.求证:以A1A2为直径的圆既与以PF2为直径的圆外切,又与以PF1为直径的圆内切.
的左、右焦点,A1,A2分别为这个双曲线的左、右顶点,P为双曲线右支上的任意一点.求证:以A1A2为直径的圆既与以PF2为直径的圆外切,又与以PF1为直径的圆内切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥![]() 中,
中, ![]() 面
面![]() ,
, ![]() 是平行四边形,
是平行四边形, ![]() ,
, ![]() ,点
,点![]() 为棱
为棱![]() 的中点,点
的中点,点![]() 在棱
在棱![]() 上,且
上,且![]() ,平面
,平面![]() 与
与![]() 交于点
交于点![]() ,则异面直线
,则异面直线![]() 与
与![]() 所成角的正切值为__________.
所成角的正切值为__________.
【答案】![]()
【解析】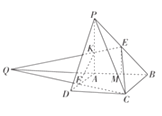
延长![]() 交
交![]() 的延长线与点Q,连接QE交PA于点K,设QA=x,
的延长线与点Q,连接QE交PA于点K,设QA=x,
由![]() ,得
,得![]() ,则
,则![]() ,所以
,所以![]() .
.
取![]() 的中点为M,连接EM,则
的中点为M,连接EM,则![]() ,
,
所以![]() ,则
,则![]() ,所以AK=
,所以AK=![]() .
.
由AD//BC,得异面直线![]() 与
与![]() 所成角即为
所成角即为![]() ,
,
则异面直线![]() 与
与![]() 所成角的正切值为
所成角的正切值为![]() .
.
【题型】填空题
【结束】
17
【题目】在极坐标系中,极点为![]() ,已知曲线
,已知曲线![]() :
: ![]() 与曲线
与曲线![]() :
: ![]() 交于不同的两点
交于不同的两点![]() ,
, ![]() .
.
(1)求![]() 的值;
的值;
(2)求过点![]() 且与直线
且与直线![]() 平行的直线
平行的直线![]() 的极坐标方程.
的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知下列命题:
①命题:x∈(0,2),3x>x3的否定是:x∈(0,2),3x≤x3;
②若f(x)=2x﹣2﹣x , 则x∈R,f(﹣x)=﹣f(x);
③若f(x)=x+ ![]() ,则x0∈(0,+∞),f(x0)=1;
,则x0∈(0,+∞),f(x0)=1;
④等差数列{an}的前n项和为Sn , 若a4=3,则S7=21;
⑤在△ABC中,若A>B,则sinA>sinB.
其中真命题是 . (只填写序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com