
科目:高中数学 来源:不详 题型:解答题
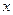 轴,焦点
轴,焦点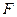 在直线
在直线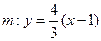 上,直线
上,直线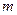 与抛物线相交于
与抛物线相交于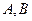 两点,
两点,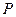 为抛物线上一动点(不同于
为抛物线上一动点(不同于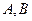 ),直线
),直线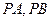 分别交该抛物线的准线
分别交该抛物线的准线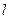 于点
于点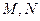 。
。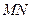 为直径的圆
为直径的圆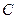 经过焦点
经过焦点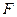 ,且当
,且当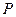 为抛物线的顶点时,圆
为抛物线的顶点时,圆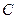 与直线
与直线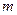 相切。
相切。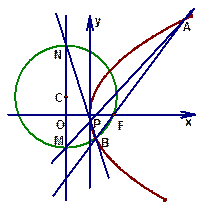
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
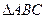 的两个顶点
的两个顶点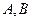 的坐标分别
的坐标分别 ,且
,且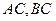 所在直线的斜率之积为
所在直线的斜率之积为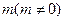 ,1)求顶点
,1)求顶点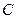 的轨迹.2)当
的轨迹.2)当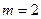 时,记顶点
时,记顶点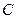 的轨迹为
的轨迹为 ,过点
,过点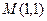 能否存在一条直线
能否存在一条直线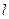 ,使
,使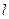 与曲线
与曲线 交于
交于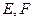 两点,且
两点,且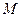 为线段
为线段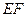 的中点,若存在求直线
的中点,若存在求直线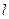 的方程,若不存在说明理由.(12分)
的方程,若不存在说明理由.(12分)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
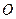 为坐标原点,点F、T、M、P分别满足
为坐标原点,点F、T、M、P分别满足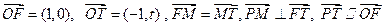 .
. 的顶点在点P的轨迹上,且点A的纵坐标
的顶点在点P的轨迹上,且点A的纵坐标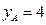 ,
, 的重心恰好为点F,
的重心恰好为点F,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com