Question

19．已知抛物线y²=2px（p＞0）的焦点为F，P、Q是抛物线上的两点，若△FPQ是边长为2的正三角形，则p的值是（　　）

• A． $2±\sqrt{3}$
• B． $2+\sqrt{3}$
• C． $\sqrt{3}±1$
• D． $\sqrt{3}-1$

Answer 1

分析 由抛物线y²=2px方程可得焦点坐标，由对称性结合三角形的边角关系可得|$\frac{p}{2}$-$\frac{1}{2p}$|=$\sqrt{3}$，解方程可得．

解答 解：y²=2px的焦点F（$\frac{p}{2}$，0），（p＞0）
∵正三角形PQF的一个顶点位于抛物线的焦点F，另外两个顶点在抛物线上，
∴正三角形PQF关于x轴对称，∴P（x₀，1），由P（x₀，1）在抛物线上可得1=2px₀，
∴x₀=$\frac{1}{2p}$，∴焦点F到直线AB的距离|$\frac{p}{2}$-$\frac{1}{2p}$|=$\sqrt{3}$，
解得：p=2±$\sqrt{3}$，
故选A．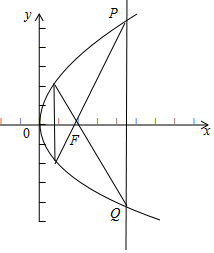

点评 本题考查抛物线的简单性质，涉及三角形的知识，属于中档题．