
| A. | 重心 | B. | 垂心 | C. | 内心 | D. | 外心 |
分析 作出图形分析位置关系,利用三垂线定理,投影定理,可得P'在底面ABC的位置.利用四心定义,准确判断.
解答 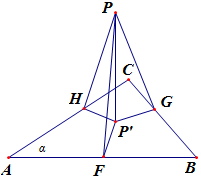 解:解法一:由题p到AB、BC、CA的距离相等,
解:解法一:由题p到AB、BC、CA的距离相等,
知|PH|=|PG|=|PF|,且PH⊥AC,PG⊥BC,PF⊥AB,
又PP'⊥平面ABC
∴∠PP'H=∠PP'G=∠PP'F=90°
∴△PP'H≌△PP'G≌△PP'F
∴P'H=P'G=P'F
又∵PP'⊥平面ABC
∴PP'⊥AB且P'F⊥AB
∴AB⊥平面PP'F
∴AB⊥P'F
同理 BC⊥P'G,AC⊥P'H
所以P'到到AB、BC、CA的距离相等,
故P'为△ABC的内心.
故选C.
解法二:由题及三垂线定理可知:
AB⊥P'F,BC⊥P'G,AC⊥P'H
又|PH|=|PG|=|PF|,由投影定理知:
P'H=P'G=P'F
所以P'到到AB、BC、CA的距离相等,
故P'为△ABC的内心.
故选C.
点评 考查三垂线定理,投影定理,线面垂直判定定理,△内心定义.考查了数形结合思想.三角形四心问题,容易概念混乱,故本题属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{15}$ | B. | 4 | C. | 2$\sqrt{3}$ | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2} | B. | {1,2,3,4} | C. | ∅ | D. | {∅} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,x2-x<0 | B. | ?x∈R,x2-x≤0 | C. | ?x∈R,x2-x<0 | D. | ?x∈R,x2-x≥0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
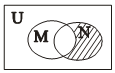 设全集U={1,2,3,4,5,6,7},集合M={1,2,3,5},N={2,4,5},则Venn图中阴影部分表示的集合是( )
设全集U={1,2,3,4,5,6,7},集合M={1,2,3,5},N={2,4,5},则Venn图中阴影部分表示的集合是( )| A. | {1,3} | B. | {4} | C. | {3,5} | D. | {5} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | π2-1 | B. | π2+1 | C. | π | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 相交且垂直 | B. | 相交但不垂直 | C. | 平行 | D. | 不确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com