
| A. | $\sqrt{15}$ | B. | 4 | C. | 2$\sqrt{3}$ | D. | 5 |
分析 根据双曲线的第二定义利用点P到右焦点的距离为2,求出P的坐标,即可求出三角形的面积.
解答 解:双曲线x2-$\frac{{y}^{2}}{3}$=1的右焦点为(2,0),右准线为x=$\frac{1}{2}$,
设双曲线上位于第一象限内的一点P坐标为(m,n),
则$\frac{2}{m-\frac{1}{2}}=2$,∴m=$\frac{3}{2}$,
∴n=$\frac{\sqrt{15}}{2}$,
∴△PF1F2的面积S=$\frac{1}{2}$|F1F2|•n=$\sqrt{15}$,
故选A.
点评 本题着重考查了三角形面积公式、双曲线的标准方程与简单几何性质等知识,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2017届湖南永州市高三高考一模考试数学(文)试卷(解析版) 题型:填空题
函数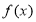 的定义域为
的定义域为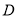 ,若存在闭区间
,若存在闭区间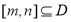 ,使得函数
,使得函数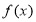 满足:(1)
满足:(1)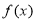 在
在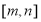 上是单调函数;(2)
上是单调函数;(2)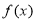 在
在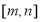 上的值域为
上的值域为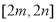 ,则称区间
,则称区间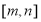 为函数
为函数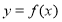 的“完美区间”.下列函数中存在“完美区间”的是________(只需填符合题意的函数序号).
的“完美区间”.下列函数中存在“完美区间”的是________(只需填符合题意的函数序号).
①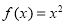 ; ②
; ②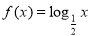 ; ③
; ③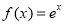 ; ④
; ④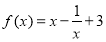 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,10) | B. | ($\frac{1}{10}$,10) | C. | ($\frac{1}{10}$,+∞) | D. | (0,$\frac{1}{10}$)∪(10,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 重心 | B. | 垂心 | C. | 内心 | D. | 外心 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com