
分析 根据题意,首先求出X=1、2、3时的概率,进而可得EX的表达式,由题意EX>1.75,可得p2-3p+3>1.75,解可得p的范围,结合p的实际意义,对求得的范围可得答案.
解答 解:由已知条件可得P(X=1)=p,
P(X=2)=(1-p)p,
P(X=3)=(1-p)2p+(1-p)3=(1-p)2,
则E(X)=P(X=1)+2P(X=2)+3P(X=3)=p+2(1-p)p+3(1-p)2=p2-3p+3>1.75,
解得p>$\frac{5}{2}$或p<$\frac{1}{2}$,又由p∈(0,1),得p∈(0,$\frac{1}{2}$).
故答案为:(0,$\frac{1}{2}$).
点评 本题考查概率的求法,是中档题,解题时要认真审题,注意解题的最后要结合概率的意义对求出的答案范围进行取舍,注意相互独立事件概率乘法公式的合理运用.


科目:高中数学 来源: 题型:解答题
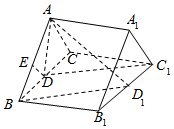 如图,在直三棱柱ABC-A1B1C1中,BA⊥CA,∠ACB=60°,AC=1,AA1=$\frac{\sqrt{3}}{2}$,点D,D1分别是BC,B1C1的中点.
如图,在直三棱柱ABC-A1B1C1中,BA⊥CA,∠ACB=60°,AC=1,AA1=$\frac{\sqrt{3}}{2}$,点D,D1分别是BC,B1C1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
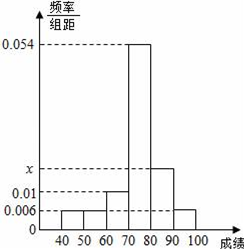 某班50位学生期中考试数学成绩的频率直方分布图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].
某班50位学生期中考试数学成绩的频率直方分布图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f (a)>f (b) | B. | f (a)=f (b) | C. | f (a)<f (b) | D. | f (a)f (b)<1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 日期 | 11月1日 | 11月2日 | 11月3日 | 11月4日 | 11月5日 |
| 温差x(℃) | 8 | 11 | 12 | 13 | 10 |
| 发芽数y(颗) | 16 | 25 | 26 | 30 | 23 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{13}{21}$ | B. | $\frac{21}{13}$ | C. | $\frac{11}{13}$ | D. | $\frac{13}{11}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充要条件 | B. | 必要不充分条件 | ||
| C. | 充分不必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com