
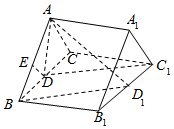
 如图,在直三棱柱ABC-A1B1C1中,BA⊥CA,∠ACB=60°,AC=1,AA1=$\frac{\sqrt{3}}{2}$,点D,D1分别是BC,B1C1的中点.
如图,在直三棱柱ABC-A1B1C1中,BA⊥CA,∠ACB=60°,AC=1,AA1=$\frac{\sqrt{3}}{2}$,点D,D1分别是BC,B1C1的中点.分析 (1)推导出四边形BDC1D1为平行四边形,从而DC1∥BD1.由此能证明DC1∥平面ABD1.
(2)过D作DE⊥AB,垂足为E,连接D1E,DD1.推导出D1D⊥AB.D1E⊥AB,从而∠D1ED是二面角D1-AB-D的平面角.由此能求出二面角D1-AB-D的大小.
解答 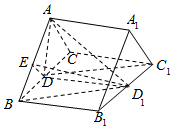 证明:(1)∵BC∥B1C1,BC=B1C1,D,D1分别是BC,B1C1的中点,
证明:(1)∵BC∥B1C1,BC=B1C1,D,D1分别是BC,B1C1的中点,
∴BD∥C1D1,BD=C1D1,∴四边形BDC1D1为平行四边形,
∴DC1∥BD1.
又DC1?平面ABD1,BD1?平面ABD1,
∴DC1∥平面ABD1.
解:(2)如图,过D作DE⊥AB,垂足为E,连接D1E,DD1.
由题意知D1D⊥平面ABC,∴D1D⊥AB.
又D1D∩DE=D,∴AB⊥平面D1DE,D1E⊥AB,
∴∠D1ED是二面角D1-AB-D的平面角.
在Rt△ABC中,∵∠ACB=60°,AC=1,∴AD=BD=1,
∴E是AB的中点,DE=$\frac{1}{2}$AC=$\frac{1}{2}$.
在Rt△D1DE中,tan∠D1ED=$\frac{{D}_{1}D}{DE}$=$\sqrt{3}$,
∴∠D1ED=60°,即二面角D1-AB-D的大小为60°.
点评 本题主要考查考生对空间几何体中线面平行、线面垂直关系的判断,二面角的平面角的作法及求法,是中档题.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 时刻 | 0:00 | 3:00 | 6:00 | 9:00 | 12:00 | 15:00 | 18:00 | 21:00 | 24:00 |
| 水深(m) | 5.0 | 7.0 | 5.0 | 3.0 | 5.0 | 7.0 | 5.0 | 3.0 | 5.0 |
| A. | 4m | B. | 5m | C. | 6m | D. | 7m |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com