
分析 由三点共线可得即$\frac{2}{a}$+$\frac{2}{b}$=1,整体代入可得2a+3b=(2a+3b)($\frac{2}{a}$+$\frac{2}{b}$),由基本不等式可得2a+3b的取值范围.
解答 解:∵三点A(2,2),B(a,0),C(0,b)(a>0,b>0)共线,
∴$\frac{0-2}{a-2}$=$\frac{b-2}{0-2}$,
即$\frac{2}{a}$+$\frac{2}{b}$=1,
∵a>0,b>0,
∴2a+3b=(2a+3b)($\frac{2}{a}$+$\frac{2}{b}$)=4+6+$\frac{4a}{b}$+$\frac{6b}{a}$≥10+2$\sqrt{\frac{4a}{b}•\frac{6b}{a}}$=10+4$\sqrt{6}$,当且仅当$\frac{4a}{b}$=$\frac{6b}{a}$取等号,
故2a+3b的取值范围为:$[{10+4\sqrt{6},+∞})$.
故答案为:$[{10+4\sqrt{6},+∞})$.
点评 本题考查三点共线和基本不等式求最值,属基础题.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:高中数学 来源: 题型:解答题
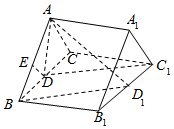 如图,在直三棱柱ABC-A1B1C1中,BA⊥CA,∠ACB=60°,AC=1,AA1=$\frac{\sqrt{3}}{2}$,点D,D1分别是BC,B1C1的中点.
如图,在直三棱柱ABC-A1B1C1中,BA⊥CA,∠ACB=60°,AC=1,AA1=$\frac{\sqrt{3}}{2}$,点D,D1分别是BC,B1C1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某制造商3月生产了一批乒乓球,随机抽取100个进行检查,测得每个球的直径(单位:mm),将数据进行分组,得到如下频率分布表:
某制造商3月生产了一批乒乓球,随机抽取100个进行检查,测得每个球的直径(单位:mm),将数据进行分组,得到如下频率分布表:| 分组 | 频数 | 频率 |
| [39.95,39.97) | 10 | 0.10 |
| [39.97,39.99) | x | 0.20 |
| [39.99,40.01) | 50 | 0.50 |
| [40.01,40.03] | 20 | y |
| 合计 | 100 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
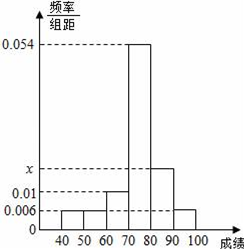 某班50位学生期中考试数学成绩的频率直方分布图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].
某班50位学生期中考试数学成绩的频率直方分布图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{13}{21}$ | B. | $\frac{21}{13}$ | C. | $\frac{11}{13}$ | D. | $\frac{13}{11}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com