
【题目】函数f(x)=Asin(ωx+φ),x∈R(其中A>0,ω>0,0<φ< ![]() )的图象与x轴相邻两个交点间的距离为
)的图象与x轴相邻两个交点间的距离为 ![]() ,且图象上一个最低点为M(
,且图象上一个最低点为M( ![]() ,﹣2). (Ⅰ)求f(x)的解析式;
,﹣2). (Ⅰ)求f(x)的解析式;
(Ⅱ)求f(x)的单调递增区间;
(Ⅲ)当x∈[ ![]() ,
, ![]() ]时,求f(x)的值域.
]时,求f(x)的值域.
【答案】解:解:(Ⅰ)由图象与x轴相邻两个交点间的距离为 ![]() ,
, ![]() =
= ![]() =
= ![]() ,∴ω=2, 再根据图象上一个最低点为M(
,∴ω=2, 再根据图象上一个最低点为M( ![]() ,﹣2),可得A=2,2×
,﹣2),可得A=2,2× ![]() +φ=
+φ= ![]() ,φ=
,φ= ![]() ,
,
∴f(x)=2sin(2x+ ![]() ).
).
(Ⅱ)令2kπ﹣ ![]() ≤2x+
≤2x+ ![]() ≤2kπ+
≤2kπ+ ![]() ,求得kπ﹣
,求得kπ﹣ ![]() ≤x≤kπ+
≤x≤kπ+ ![]() ,k∈Z;
,k∈Z;
(Ⅲ)当x∈[ ![]() ,
, ![]() ]时,
]时, ![]() ≤2x+
≤2x+ ![]() ≤
≤ ![]() ,∴sin(2x+
,∴sin(2x+ ![]() )∈[﹣1,2],故函数的值域为[﹣1,2].
)∈[﹣1,2],故函数的值域为[﹣1,2].
【解析】(Ⅰ)由周期求得ω,由最低点的坐标结合五点法作图求得A及φ的值,可得函数f(x)的解析式.(Ⅱ)由条件利用正弦函数的单调性,求得f(x)的单调递增区间.(Ⅲ)当x∈[ ![]() ,
, ![]() ],利用正弦函数的定义域和值域,求得f(x)的值域.
],利用正弦函数的定义域和值域,求得f(x)的值域.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga(x+1),g(x)=loga(4﹣2x),a>0且a≠1.
(1)求函数y=f(x)﹣g(x)的定义域;
(2)求使不等式f(x)>g(x)成立的实数x的取值范围;
(3)求函数y=2f(x)﹣g(x)﹣f(1)的零点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知全集U=R,集合A={x|1<x<4},B={x|x≤3m﹣4或x≥8+m}(m<6)
(1)若m=2,求A∩(UB)
(2)若A∩(UB)=,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型超市拟对店庆当天购物满![]() 元的顾客进行回馈奖励.规定:顾客转动十二等分且质地均匀的圆形转盘(如图),待转盘停止转动时,若指针指向扇形区域,则顾客可领取此区域对应面额(单位:元)的超市代金券.假设转盘每次转动的结果互不影响.
元的顾客进行回馈奖励.规定:顾客转动十二等分且质地均匀的圆形转盘(如图),待转盘停止转动时,若指针指向扇形区域,则顾客可领取此区域对应面额(单位:元)的超市代金券.假设转盘每次转动的结果互不影响.
(Ⅰ)若![]() ,求顾客转动一次转盘获得
,求顾客转动一次转盘获得![]() 元代金券的概率;
元代金券的概率;
(Ⅱ)某顾客可以连续转动两次转盘并获得相应奖励,当![]() 时,求该顾客第一次获得代金券的面额不低于第二次获得代金券的面额的概率;
时,求该顾客第一次获得代金券的面额不低于第二次获得代金券的面额的概率;
(Ⅲ)记顾客每次转动转盘获得代金券的面额为![]() ,当
,当![]() 取何值时,
取何值时, ![]() 的方差最小?
的方差最小?
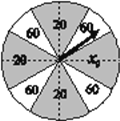
(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等比数列![]() 中,
中, ![]() 分别是下表中第
分别是下表中第![]() 行中的某一个数,且
行中的某一个数,且![]() 中任何两个数不在下表的同一列中.
中任何两个数不在下表的同一列中.
第 | 第 | 第 | |
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
(1)求数列![]() 的通项公式;
的通项公式;
(2)设![]() ,求数列
,求数列![]() 的前
的前![]() 项和.
项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业招聘中,依次进行A科、B科考试,当A科合格时,才可考B科,且两科均有一次补考机会,两科都合格方通过.甲参加招聘,已知他每次考A科合格的概率均为 ![]() ,每次考B科合格的概率均为
,每次考B科合格的概率均为 ![]() .假设他不放弃每次考试机会,且每次考试互不影响.
.假设他不放弃每次考试机会,且每次考试互不影响.
(1)求甲恰好3次考试通过的概率;
(2)记甲参加考试的次数为ξ,求ξ的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=8 cm,AB=10 cm,点P由C出发以每秒2 cm的速度沿线段CA向点A运动(不运动至A点),⊙O的圆心在BP上,且⊙O分别与AB、AC相切,当点P运动2 s时,⊙O的半径是( )
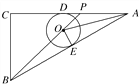
A. ![]() cm B.
cm B. ![]() cm C.
cm C. ![]() cm D. 2 cm
cm D. 2 cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com