
【题目】某企业招聘中,依次进行A科、B科考试,当A科合格时,才可考B科,且两科均有一次补考机会,两科都合格方通过.甲参加招聘,已知他每次考A科合格的概率均为 ![]() ,每次考B科合格的概率均为
,每次考B科合格的概率均为 ![]() .假设他不放弃每次考试机会,且每次考试互不影响.
.假设他不放弃每次考试机会,且每次考试互不影响.
(1)求甲恰好3次考试通过的概率;
(2)记甲参加考试的次数为ξ,求ξ的分布列和期望.
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】某公司即将推车一款新型智能手机,为了更好地对产品进行宣传,需预估市民购买该款手机是否与年龄有关,现随机抽取了50名市民进行购买意愿的问卷调查,若得分低于60分,说明购买意愿弱;若得分不低于60分,说明购买意愿强,调查结果用茎叶图表示如图所示.

(1)根据茎叶图中的数据完成![]() 列联表,并判断是否有95%的把握认为市民是否购买该款手机与年龄有关?
列联表,并判断是否有95%的把握认为市民是否购买该款手机与年龄有关?

(2)从购买意愿弱的市民中按年龄进行分层抽样,共抽取5人,从这5人中随机抽取2人进行采访,求这2人都是年龄大于40岁的概率.
附: 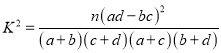 .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx+φ),x∈R(其中A>0,ω>0,0<φ< ![]() )的图象与x轴相邻两个交点间的距离为
)的图象与x轴相邻两个交点间的距离为 ![]() ,且图象上一个最低点为M(
,且图象上一个最低点为M( ![]() ,﹣2). (Ⅰ)求f(x)的解析式;
,﹣2). (Ⅰ)求f(x)的解析式;
(Ⅱ)求f(x)的单调递增区间;
(Ⅲ)当x∈[ ![]() ,
, ![]() ]时,求f(x)的值域.
]时,求f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=![]() ,AC=3, BC=2,P是△ABC内的一点.
,AC=3, BC=2,P是△ABC内的一点.
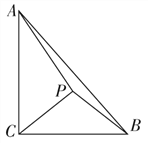
(1)若P是等腰直角三角形PBC的直角顶点,求PA的长;
(2)若∠BPC=![]() ,设∠PCB=θ,求△PBC的面积S(θ)的解析式,并求S(θ)的最大值.
,设∠PCB=θ,求△PBC的面积S(θ)的解析式,并求S(θ)的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个人有n把钥匙,其中只有一把可以打开房门,他随意的进行试开,若试开过的钥匙放在一边,试开次数X为随机变量,则P(X=k)=( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现需要设计一个仓库,它由上下两部分组成,上部分的形状是正四棱锥![]() ,下部分的形状是正四棱柱
,下部分的形状是正四棱柱![]() (如图所示),并要求正四棱柱的高
(如图所示),并要求正四棱柱的高![]() 是正四棱锥的高
是正四棱锥的高![]() 的4倍.
的4倍.

(1)若![]() 则仓库的容积是多少?
则仓库的容积是多少?
(2)若正四棱锥的侧棱长为![]() ,则当
,则当![]() 为多少时,仓库的容积最大?
为多少时,仓库的容积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
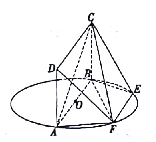
【题目】如图, ![]() 为圆
为圆![]() 的直径,点
的直径,点![]() 在圆
在圆![]() 上,且
上,且![]() ,矩形
,矩形![]() 所在的平面和圆
所在的平面和圆![]() 所在的平面垂直,且
所在的平面垂直,且![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在了点
上是否存在了点![]() ,使得
,使得![]() 平面
平面![]() ?并说明理由.
?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com