
分析 将已知移项后,利用和差化积公式化简,整理,利用同角三角函数基本关系式即可证明.
解答 证明:cos2A+cos2C=2cos2B,
⇒cos2A-cos2B=cos2B-cos2C,
⇒2sin(A+B)sin(A-B)=2sin(B+C)sin(B-C),
⇒sinCsin(A-B)=sinAsin(B-C),
⇒sinC(sinAcosB-cosAsinB)=sinA(sinBcosC-cosBsinC),
⇒2sinAcosBsinC=cosAsinBsinC+sinAsinBcosC,(两边同除以sinAsinBsinC)
⇒$\frac{2}{tanB}=\frac{1}{tanA}+\frac{1}{tanC}$.
得证.
点评 本题主要考查了三角函数恒等式的证明,考查了三角函数恒等变换的应用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | -$\frac{17}{40}$ | B. | -$\frac{5}{16}$ | C. | -$\frac{34}{45}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
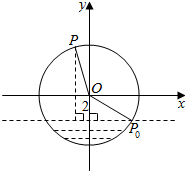 如图,半径为4m的水轮绕着圆心O逆时针做匀速圆周运动,每分钟转动4圈,水轮圆心O距离水面2m,如果当水轮上点P从离开水面的时刻(P0)开始计算时间.
如图,半径为4m的水轮绕着圆心O逆时针做匀速圆周运动,每分钟转动4圈,水轮圆心O距离水面2m,如果当水轮上点P从离开水面的时刻(P0)开始计算时间.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | $\frac{{\sqrt{3}}}{3}$ | C. | 1 | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2,3) | B. | (-1,-2,3) | C. | (-1,2,-3) | D. | (-1,-2,-3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
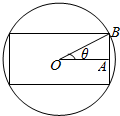 把截面半径为5的圆形木头锯成面积为y的矩形木料,如图,点O为圆心,OA⊥OB,设∠AOB=θ,把面积y表示为θ的表达式,则有( )
把截面半径为5的圆形木头锯成面积为y的矩形木料,如图,点O为圆心,OA⊥OB,设∠AOB=θ,把面积y表示为θ的表达式,则有( )| A. | y=50cos2θ | B. | y=25sinθ | C. | y=25sin2θ | D. | y=50sin2θ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com