
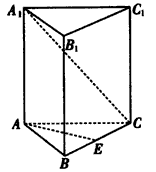
| 解:过E作EN⊥AC于N,连结EF, (1)如图1,连结NF、AC1, 由直棱柱的性质知,底面ABC⊥侧面A1C, 又底面ABC∩侧面A1C=AC,EN  底面ABC, 底面ABC,所以EN⊥侧面A1C,NF为EF在侧面A1C内的射影, 在Rt△CNE中,CN=CEcos60°=1, 则由  ,得NF∥AC1, ,得NF∥AC1,又AC1⊥A1C, 故NF⊥A1C, 由三垂线定理知EF⊥A1C。 |
 |
| (2)如图2,连结AF,过N作NM⊥AF于M,连结ME, 由(1)知EN⊥侧面A1C, 根据三垂线定理得EM⊥AF, 所以∠EMN是二面角C-AF-E的平面角,即∠EMN=θ, 设∠FAC=α,则0°<α≤45°, 在Rt△CNE中,NE=EC·sin60°=  , ,在Rt△AMN中,MN=AN·sinα-3sinα, 故  , ,又0°<α≤45°, ∴  , ,故当  , ,即当α=45°时,tanθ达到最小值,  ,此时F与C1重合. ,此时F与C1重合. |
 |


 阶梯计算系列答案
阶梯计算系列答案科目:高中数学 来源: 题型:
 如图,已知正三棱柱ABC-A1B1C1各棱长都为a,P为线段A1B上的动点.
如图,已知正三棱柱ABC-A1B1C1各棱长都为a,P为线段A1B上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知正三棱柱ABC-A1B1C1的底面边长为2cm,高位5cm,一质点自A点出发,沿着三棱柱的侧面绕行两周到达A1点的最短路线的长为
如图,已知正三棱柱ABC-A1B1C1的底面边长为2cm,高位5cm,一质点自A点出发,沿着三棱柱的侧面绕行两周到达A1点的最短路线的长为查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知正三棱柱ABC-A1B1C1的各条棱长都为a,P为A1B上的点.
如图,已知正三棱柱ABC-A1B1C1的各条棱长都为a,P为A1B上的点.| A1P |
| PB |
| A1P |
| PB |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2011•重庆三模)如图,已知正三棱柱ABC-A1B1C1的所有棱长均为a,截面AB1C和A1BC1相交于DE,则三棱锥B-B1DE的体积为
(2011•重庆三模)如图,已知正三棱柱ABC-A1B1C1的所有棱长均为a,截面AB1C和A1BC1相交于DE,则三棱锥B-B1DE的体积为
| ||
| 48 |
| ||
| 48 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com