
分析 (1)由$\left\{\begin{array}{l}f(1)=1\\ f(-2)=4\end{array}\right.$,得$\left\{\begin{array}{l}{\frac{a}{1+b}=1}\\{\frac{-2a}{-2+b}=4}\end{array}\right.$,解得a,b的值,
方法1:假设存在常数c符合要求,即f(x)+f(c-x)=4,x≠-1成立,特别当x=0时,解得c的值,然后证明
f(x)+f(-2-x)=4,x≠-1恒成立,当x≠-1时,则f(x)+f(-2-x)=4,故存在常数c=-2,满足题设要求;
方法2:假设存在常数c符合要求,即f(x)+f(c-x)=4,x≠-1成立,则$\frac{2x}{x+1}+\frac{2(c-x)}{c-x+1}=4$,变形得,-x2+(c-1)x+c=-x2+(c-1)x+2(c+1),整理得c的值,故存在常数c=-2,满足题设要求;
(2)不等式f(x)≤$\frac{2m}{(x+1)|x-m|}$即为$\frac{2x}{x+1}≤$$\frac{2m}{(x+1)|x-m|}$对x∈[1,2]恒成立,即$x≤\frac{m}{|x-m|}$对x∈[1,2]恒成立,则0<m<1或m>2,进一步化为$|x-m|≤\frac{m}{x}$对x∈[1,2]恒成立,即mx-m≤x2≤mx+m对x∈[1,2]恒成立,再分类讨论①当x=1时,$\frac{1}{2}≤m<1$或m>2,②当x≠1时,求出0<m<1或2<m≤4,综上,实数m的取值范围可求.
解答 解:(1)由$\left\{\begin{array}{l}f(1)=1\\ f(-2)=4\end{array}\right.$,得$\left\{\begin{array}{l}{\frac{a}{1+b}=1}\\{\frac{-2a}{-2+b}=4}\end{array}\right.$,解得$\left\{\begin{array}{l}a=2\\ b=1\end{array}\right.$.
∴$f(x)=\frac{2x}{x+1}$(x≠-1).
方法1:假设存在常数c符合要求,即f(x)+f(c-x)=4,x≠-1成立.
特别当x=0时有f(0)+f(c)=4,即$\frac{2c}{c+1}=4$,解得c=-2.
下面证明f(x)+f(-2-x)=4,x≠-1恒成立.事实上,当x≠-1时,
则f(x)+f(-2-x)=$\frac{2x}{x+1}+\frac{2(-2-x)}{(-2-x)+1}=\frac{2x}{x+1}+\frac{-4-2x}{-x-1}$=$\frac{4x+4}{x+1}=4$.
∴存在常数c=-2,满足题设要求;
方法2:假设存在常数c符合要求,即f(x)+f(c-x)=4,x≠-1成立.
则$\frac{2x}{x+1}+\frac{2(c-x)}{c-x+1}=4$,
即$\frac{c-x}{c-x+1}=2-\frac{x}{x+1}$,
变形得,-x2+(c-1)x+c=-x2+(c-1)x+2(c+1),
整理得,c=-2.
∴存在常数c=-2,满足题设要求;
(2)不等式f(x)≤$\frac{2m}{(x+1)|x-m|}$即为$\frac{2x}{x+1}≤$$\frac{2m}{(x+1)|x-m|}$对x∈[1,2]恒成立,
即$x≤\frac{m}{|x-m|}$对x∈[1,2]恒成立,
故必有0<m<1或m>2.
在0<m<1或m>2下,问题化为$|x-m|≤\frac{m}{x}$对x∈[1,2]恒成立,
即mx-m≤x2≤mx+m对x∈[1,2]恒成立,
①当x=1时,$\frac{1}{2}≤m<1$或m>2.
②当x≠1时,$m≥\frac{{x}^{2}}{x+1}$且$m≤\frac{{x}^{2}}{x-1}$对x∈[1,2]恒成立,
对于$m≥\frac{{x}^{2}}{x+1}$对x∈[1,2]恒成立,等价于$m≥(\frac{{x}^{2}}{x+1})_{max}$,
令t=x+1,x∈[1,2],则x=t-1,t∈(2,3],
$\frac{{x}^{2}}{x+1}=\frac{(t-1)^{2}}{t}=t+\frac{1}{t}-2$,t∈(2,3]递增,
∴$(\frac{{x}^{2}}{x+1})_{max}=\frac{4}{3}$,
即$m≥\frac{4}{3}$,结合0<m<1或m>2,
∴m>2.
对于$m≤\frac{{x}^{2}}{x-1}$对x∈[1,2]恒成立,等价于$m≤(\frac{{x}^{2}}{x-1})_{min}$,
令t=x-1,x∈[1,2],则x=t+1,t∈(0,1],
$\frac{{x}^{2}}{x-1}=\frac{(t+1)^{2}}{t}=t+\frac{1}{t}+2$,t∈(0,1]递减,
∴$(\frac{{x}^{2}}{x-1})_{min}=4$,
∴m≤4,结合0<m<1或m>2,
∴0<m<1或2<m≤4,
综上,实数m的取值范围为2<m≤4.
点评 本题考查了函数恒成立问题,考查利用赋值法求解恒成立问题,考查函数的最值问题,关键是审清题意,合理转化,注意赋值法求解恒成立问题时,应需要验证其恒成立,是难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 云南省2014年全省高中男生身高统计调查显示:全省男生的身高服从正态分布N(170.5.16).高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于175.5cm和187.5cm之间,将测量结果按如下方式分成6组:第 一组[157.5,162.5),第二组[162.5,167.5),…第 6 组(182.5,187.5],按上述分组方法得到的频率分布直方图如图所示.
云南省2014年全省高中男生身高统计调查显示:全省男生的身高服从正态分布N(170.5.16).高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于175.5cm和187.5cm之间,将测量结果按如下方式分成6组:第 一组[157.5,162.5),第二组[162.5,167.5),…第 6 组(182.5,187.5],按上述分组方法得到的频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\frac{3\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | $\frac{\sqrt{13}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
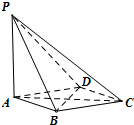 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com