
设a,b,c是正实数,求证:aabbcc≥(abc)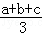 .
.
 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源:[同步]2014年湘教版必修二 3.1 弧度制与任意角练习卷1(解析版) 题型:填空题
(5分)已知点P(tanα,cosα)在第三象限,则角α的终边在第 象限.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版必修三 7.1 解析几何初步练习卷(解析版) 题型:选择题
(4分)若点A(a,0),B(0,b),C(1,﹣1)(a>0,b<0)三点共线,则a﹣b的最小值等于( )
A.4 B.2 C.1 D.0
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教B版选修4-5 2.3平均值不等式练习卷(解析版) 题型:选择题
已知实数a,b,c,d满足a+b+c+d=3,a2+2b2+4c2+4d2=5则a的最大值为( )
A.1 B.2 C.3 D..4
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教B版选修4-5 2.3平均值不等式练习卷(解析版) 题型:选择题
(2007•北京)如果正数a,b,c,d满足a+b=cd=4,那么( )
A.ab≤c+d且等号成立时a,b,c,d的取值唯一
B.ab≥c+d且等号成立时a,b,c,d的取值唯一
C.ab≤c+d且等号成立时a,b,c,d的取值不唯一
D.ab≥c+d且等号成立时a,b,c,d的取值不唯一
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教B版选修4-5 2.2排序不等式练习卷(解析版) 题型:解答题
已知a,b,c为正数,用排序不等式证明:2(a3+b3+c3)≥a2(b+c)+b2(a+c)+c2(a+b).
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教B版选修4-5 1.4绝对值的三角不等式练习卷(解析版) 题型:填空题
(2013•天河区三模)以下三个命题:
①若|a﹣b|<1,则|a|<|b|+1;
②若a,b∈R,则|a+b|﹣2|a|≤|a﹣b|;
③若|x|<2,|y|>3,则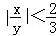 ,
,
其中正确命题的序号是 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教B版选修4-5 1.3绝对值不等式的解法练习卷(解析版) 题型:选择题
(2014•江西二模)若存在x∈R,使|2x﹣a|+2|3﹣x|≤1成立,则实数a的取值范围是( )
A.[2,4] B.(5,7) C.[5,7] D.(﹣∞,5]∪[7,+∞)
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教B版选修2-1 2.1曲线与方程练习卷(解析版) 题型:选择题
(2014•安徽模拟)直线x﹣3y﹣1=0的倾斜角为α,曲线y=lnx在(x0,lnx0)处的切线的倾斜角为2α,则x0的值是( )
A.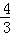 B.
B. C.
C.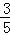 D.
D.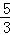
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com