
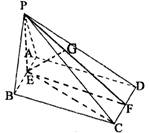
(08年惠州一中三模理) 如图,四棱锥P―ABCD的底面是AB=2,BC=![]() 的矩形,侧面PAB是等边三角形,且侧面PAB⊥底面ABCD
的矩形,侧面PAB是等边三角形,且侧面PAB⊥底面ABCD
(I)证明:侧面PAB⊥侧面PBC;
(II)求侧棱PC与底面ABCD所成的角;
(III)求直线AB与平面PCD的距离.

解析:(I)证明:在矩形ABCD中,BC⊥AB
又∵面PAB⊥底面ABCD侧面PAB∩底面ABCD=AB
∴BC⊥侧面PAB 又∵BC![]() 侧面PBC
侧面PBC
∴侧面PAB⊥侧面PBC)
(II)解:取AB中点E,连结PE、CE
又∵△PAB是等边三角形 ∴PE⊥AB
又∵侧面PAB⊥底面ABCD,∴PE⊥面ABCD
∴∠PCE为侧棱PC与底面ABCD所成角
![]()
在Rt△PEC中,∠PCE=45°为所求
(Ⅲ)解:在矩形ABCD中,AB//CD
∵CD![]() 侧面PCD,AB
侧面PCD,AB![]() 侧面PCD,∴AB//侧面PCD
侧面PCD,∴AB//侧面PCD
取CD中点F,连EF、PF,则EF⊥AB
又∵PE⊥AB ∴AB⊥平面PEF 又∵AB//CD
∴CD⊥平面PEF ∴平面PCD⊥平面PEF
作EG⊥PF,垂足为G,则EC⊥平面PCD
在Rt△PEF中,EG=![]() 为所求.
为所求.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:
(08年惠州一中三模理) 有A,B,C,D四个城市,它们都有一个著名的旅游点依此记为a,b,c,d把A,B,C,D和a,b,c,d分别写成左、右两列,现在一名旅游爱好者随机用4条线把左右全部连接起来,构成“一一对应”,已知连对的得2分,连错的得0分;
(1)求该爱好者得分的分布列;
(2)求所得分的数学期望?
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年惠州一中三模理) 已知函数![]() 的定义域为R,对任意的
的定义域为R,对任意的![]() 都满足
都满足![]() ,当
,当![]() 时,
时,![]() .
.
(1)判断并证明![]() 的单调性和奇偶性
的单调性和奇偶性
(2)是否存在这样的实数m,当![]() 时,使不等式
时,使不等式
![]()
对所有![]() 恒成立,如存在,求出m的取值范围;若不存在,说明理由.
恒成立,如存在,求出m的取值范围;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com