
【题目】在集合![]() 的子集中选出4个不同的子集,需同时满足以下两个条件:
的子集中选出4个不同的子集,需同时满足以下两个条件:
(1)![]() ,
,![]() 都要选出;(2)对选出的任意两个子集
都要选出;(2)对选出的任意两个子集![]() 和
和![]() ,必有
,必有![]() 或
或![]() ;
;
那么具有_______种不同的选法;
【答案】36
【解析】
根据题意对集合![]() 集合中的元素个数进行分类讨论,确定B相应的结果,然后应用计数原理得到答案.
集合中的元素个数进行分类讨论,确定B相应的结果,然后应用计数原理得到答案.
因为![]() ,
,![]() 都要选出,而所有任意两个子集的组合必须有包含关系,
都要选出,而所有任意两个子集的组合必须有包含关系,
所以需要选择的子集有![]() 和
和![]() ,
,
因为对任意的子集![]() 和
和![]() 有,
有,![]() ,
,
所以只需对选出的子集![]() 和
和![]() 有,
有,![]() 或
或![]() ,
,
不妨设![]() .且
.且![]() 和
和![]() 均为
均为![]() 的非空真子集.
的非空真子集.
若集合![]() 元素个数为1,有
元素个数为1,有![]() 四种选法,
四种选法,
(1)子集![]() 元素个数为2,当子集
元素个数为2,当子集![]() 为
为![]() 时,子集
时,子集![]() 的2个元素中必须包含
的2个元素中必须包含![]() ,
,
剩下的一个从![]() 中选取有三种选法,所以这种子集的选取方法共有4×3=12种.
中选取有三种选法,所以这种子集的选取方法共有4×3=12种.
(2)子集![]() 中包含3个元素,同理三个元素必须有一个与子集
中包含3个元素,同理三个元素必须有一个与子集![]() 中的元素相同,共有4×3=12种.
中的元素相同,共有4×3=12种.
若集合![]() 元素个数为2,有6种取法,子集
元素个数为2,有6种取法,子集![]() 必须有3个元素且必须包含前面一个子集的两个元素,
必须有3个元素且必须包含前面一个子集的两个元素,
有两种取法,所以这种方法有6×2=12种
综上一共有12+12+12=36种
故答案为:36.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】某商店投入38万元经销某种纪念品,经销时间共60天,为了获得更多的利润,商店将每天获得的利润投入到次日的经营中,市场调研表明,该商店在经销这第一产品期间第![]() 天的利润
天的利润 (单位:万元,
(单位:万元,![]() ),记第
),记第![]() 天的利润率
天的利润率![]() ,例如
,例如![]() .
.
(1)求![]() 的值;
的值;
(2)求第![]() 天的利润率
天的利润率![]() ;
;
(3)该商店在经销此纪念品期间,哪一天的利润率最大?并求该天的利润率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知![]() 为等边三角形,
为等边三角形,![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,平面
,平面![]() 平面ABD,点E与点D在平面ABC的同侧,且
平面ABD,点E与点D在平面ABC的同侧,且![]() ,
,![]() .点F为AD中点,连接EF.
.点F为AD中点,连接EF.

(1)求证:![]() 平面ABC;
平面ABC;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系上,有一点列![]() ,设点
,设点![]() 的坐标
的坐标![]() (
(![]() ),其中
),其中![]() . 记
. 记![]() ,
,![]() ,且满足
,且满足![]() (
(![]() ).
).
(1)已知点![]() ,点
,点![]() 满足
满足![]() ,求
,求![]() 的坐标;
的坐标;
(2)已知点![]() ,
,![]() (
(![]() ),且
),且![]() (
(![]() )是递增数列,点
)是递增数列,点![]() 在直线
在直线![]() :
:![]() 上,求
上,求![]() ;
;
(3)若点![]() 的坐标为
的坐标为![]() ,
,![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年6月,国内的![]() 运营牌照开始发放.从
运营牌照开始发放.从![]() 到
到![]() ,我们国家的移动通信业务用了不到20年的时间,完成了技术上的飞跃,跻身世界先进水平.为了解高校学生对
,我们国家的移动通信业务用了不到20年的时间,完成了技术上的飞跃,跻身世界先进水平.为了解高校学生对![]() 的消费意愿,2019年8月,从某地在校大学生中随机抽取了1000人进行调查,样本中各类用户分布情况如下:
的消费意愿,2019年8月,从某地在校大学生中随机抽取了1000人进行调查,样本中各类用户分布情况如下:
用户分类 | 预计升级到 | 人数 |
早期体验用户 | 2019年8月至2019年12月 | 270人 |
中期跟随用户 | 2020年1月至2021年12月 | 530人 |
后期用户 | 2022年1月及以后 | 200人 |
我们将大学生升级![]() 时间的早晚与大学生愿意为
时间的早晚与大学生愿意为![]() 套餐支付更多的费用作比较,可得出下图的关系(例如早期体验用户中愿意为
套餐支付更多的费用作比较,可得出下图的关系(例如早期体验用户中愿意为![]() 套餐多支付5元的人数占所有早期体验用户的
套餐多支付5元的人数占所有早期体验用户的![]() ).
).

(1)从该地高校大学生中随机抽取1人,估计该学生愿意在2021年或2021年之前升级到![]() 的概率;
的概率;
(2)从样本的早期体验用户和中期跟随用户中各随机抽取1人,以![]() 表示这2人中愿意为升级
表示这2人中愿意为升级![]() 多支付10元或10元以上的人数,求
多支付10元或10元以上的人数,求![]() 的分布列和数学期望;
的分布列和数学期望;
![]() 套餐,能否认为样本中早期体验用户的人数有变化?说明理由.
套餐,能否认为样本中早期体验用户的人数有变化?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)若![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,求
两点,求![]() ;
;
(2)若![]() ,求曲线
,求曲线![]() 上的点到直线
上的点到直线![]() 的距离的最小值.
的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A是圆锥的顶点,![]() 是圆锥底面的直径,C是底面圆周上一点,
是圆锥底面的直径,C是底面圆周上一点,![]() ,
,![]() 与底面所成角的大小为60°,过点A作截面
与底面所成角的大小为60°,过点A作截面![]() ,截去部分后的几何体如图所示.
,截去部分后的几何体如图所示.
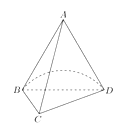
(1)求异面直线![]() 与
与![]() 所成角的大小;
所成角的大小;
(2)求该几何体的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com