
| 项目 | 生产成本 | 检验费/次 | 调试费 | 出厂价 |
| 金额(元) | 1000 | 100 | 200 | 3000 |
分析 (Ⅰ)先求出每台仪器不能出厂的概率,由此利用对立事件概率计算公式能求出每台仪器能出厂的概率.
(Ⅱ)利用相互独立事件概率乘法公式能求出生产一台仪器利润为1600的概率.
(Ⅲ)X可取3800,3500,3200,500,200,-2800.分别求出相应的概率,由此能求出X的分布列和数学期望.
解答 解:(Ⅰ)记每台仪器不能出厂为事件A,
则$P(A)=(1-\frac{3}{4})(1-\frac{4}{5})=\frac{1}{20}$,
所以每台仪器能出厂的概率$P(\overline A)=1-\frac{1}{20}=\frac{19}{20}$.
(Ⅱ)生产一台仪器利润为1600的概率:
$P=(1-\frac{3}{4})×\frac{4}{5}=\frac{1}{5}$.
(Ⅲ)X可取3800,3500,3200,500,200,-2800.
$P(X=3800)=\frac{3}{4}×\frac{3}{4}=\frac{9}{16}$,
$P(X=3500)=C_2^1×\frac{1}{5}×\frac{3}{4}=\frac{3}{10}$,
$P(X=3200)={(\frac{1}{5})^2}=\frac{1}{25}$,
$P(X=500)=C_2^1×\frac{3}{4}×(\frac{1}{4}×\frac{1}{5})=\frac{3}{40}$,
$P(X=200)=C_2^1×\frac{1}{5}×(\frac{1}{4}×\frac{1}{5})=\frac{1}{50}$,
$P(X=-2800)={(\frac{1}{4}×\frac{1}{5})^2}=\frac{1}{400}$.
X的分布列为:
| X | 3800 | 3500 | 3200 | 500 | 200 | -2800 |
| P | $\frac{9}{16}$ | $\frac{3}{10}$ | $\frac{1}{25}$ | $\frac{3}{40}$ | $\frac{1}{50}$ | $\frac{1}{400}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列及数学期望的求法,考查推理论证能力、运算求解能力,考查函数与方程思想、化归转化思想,是中档题.


科目:高中数学 来源: 题型:解答题
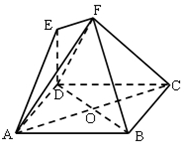 如图,多面体EF-ABCD中,四边形ABCD是菱形,AB=4,∠BAD=60°,AC,BD相交于O,EF∥AC,点E在平面ABCD上的射影恰好是线段AO的中点.
如图,多面体EF-ABCD中,四边形ABCD是菱形,AB=4,∠BAD=60°,AC,BD相交于O,EF∥AC,点E在平面ABCD上的射影恰好是线段AO的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2016) | B. | (-2018,-2016) | ||
| C. | (-2018,+∞) | D. | (-∞,-2018)∪(-2016,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{9}$ | C. | 3 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在一段直行的公路上方D处有一测速球机,在球机下方路面有A,B,C三个测速点,测得球机距点A为14米,AB=10米,球机探测点B和C的俯角分别为60°和45°,现有一小汽车从A地到C地用时1秒,则小汽车经过AC这段路程的平均速度约为18.1米/秒.(结果精确到0.1,参考数据$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)
如图,在一段直行的公路上方D处有一测速球机,在球机下方路面有A,B,C三个测速点,测得球机距点A为14米,AB=10米,球机探测点B和C的俯角分别为60°和45°,现有一小汽车从A地到C地用时1秒,则小汽车经过AC这段路程的平均速度约为18.1米/秒.(结果精确到0.1,参考数据$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 894升 | B. | 1170升 | C. | 1275米 | D. | 1467米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com