
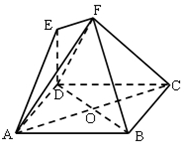
 如图,多面体EF-ABCD中,四边形ABCD是菱形,AB=4,∠BAD=60°,AC,BD相交于O,EF∥AC,点E在平面ABCD上的射影恰好是线段AO的中点.
如图,多面体EF-ABCD中,四边形ABCD是菱形,AB=4,∠BAD=60°,AC,BD相交于O,EF∥AC,点E在平面ABCD上的射影恰好是线段AO的中点.分析 (Ⅰ)取AO的中点H,连结EH,证明EH⊥BD,AC⊥BD,即BD⊥平面ACF
(Ⅱ)由(Ⅰ)知EH⊥平面ABCD,以H为原点,如图所示建立空间直角坐标系H-xyz,
由EH⊥平面ABCD,得∠EAH为AE与平面ABCD所成的角,即∠EAH=45°则$AO=2\sqrt{3},AH=\sqrt{3},EH=\sqrt{3}$各点坐标分别为$H(0,0,0),A(\sqrt{3},0,0),D(-\sqrt{3},-2,0),O(-\sqrt{3},0,0)$,E(0,0,$\sqrt{3}$),求出法向量即可求解.
解答 解:(Ⅰ)取AO的中点H,连结EH,则EH⊥平面ABCD
∵BD在平面ABCD内,∴EH⊥BD…(2分)
又菱形ABCD中,AC⊥BD 且EH∩AC=H,EH、AC在平面EACF内
∴BD⊥平面EACF,即BD⊥平面ACF…(5分)
(Ⅱ)由(Ⅰ)知EH⊥平面ABCD,以H为原点,如图所示建立空间直角坐标系H-xyz…(6分)
∵EH⊥平面ABCD,∴∠EAH为AE与平面ABCD所成的角,
即∠EAH=45°,又菱形ABCD的边长为4,则$AO=2\sqrt{3},AH=\sqrt{3},EH=\sqrt{3}$
各点坐标分别为$H(0,0,0),A(\sqrt{3},0,0),D(-\sqrt{3},-2,0),O(-\sqrt{3},0,0)$,E(0,0,$\sqrt{3}$)…(7分)
易知$\overrightarrow{HE}$为平面ABCD的一个法向量,记$\overrightarrow n$=$\overrightarrow{HE}=(0,0,\sqrt{3})$,$\overrightarrow{AO}$=$({-2\sqrt{3},0,0})$,$\overrightarrow{DE}$=$({\sqrt{3},2,\sqrt{3}})$
∵EF∥AC,∴$\overrightarrow{EF}$=$λ\overrightarrow{AO}=({-2\sqrt{3}λ,0,0})$…(8分)
设平面DEF的一个法向量为$\overrightarrow m=({x,y,z}),则\overrightarrow m⊥\overrightarrow{DE},\overrightarrow m⊥\overrightarrow{EF}$(注意:此处$\overrightarrow{EF}$可以用$\overrightarrow{AO}$替代)
即 $\overrightarrow m•\overrightarrow{DE}$=$\sqrt{3}x+2y+\sqrt{3}z=0$,$\overrightarrow m•\overrightarrow{EF}=-2\sqrt{3}λx=0$
令$y=\sqrt{3},则x=0,z=-2$,则,∴$\overrightarrow m=({0,\sqrt{3},-2})$…(9分)
∴$cos\left?{\overrightarrow n,\overrightarrow m}\right>=\frac{\overrightarrow n•\overrightarrow m}{{|{\overrightarrow n}|•|{\overrightarrow m}|}}=\frac{{-2\sqrt{3}}}{{\sqrt{3}•\sqrt{7}}}=-\frac{{2\sqrt{7}}}{7}$
平面DEF与平面ABCD所成角(锐角)的余弦值为$\frac{{2\sqrt{7}}}{7}$.…(12分)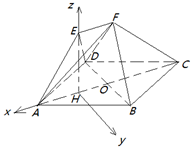
点评 本题考查了空间线面垂直、向量法求二面角,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
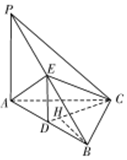 如图,已知三棱锥P-ABC中,PA⊥AC,PC⊥BC,E为PB中点,D为AB的中点,且△ABE为正三角形.
如图,已知三棱锥P-ABC中,PA⊥AC,PC⊥BC,E为PB中点,D为AB的中点,且△ABE为正三角形.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{16}{5}$ | B. | $\frac{16}{15}$ | C. | $\frac{16}{29}$ | D. | $\frac{16}{31}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
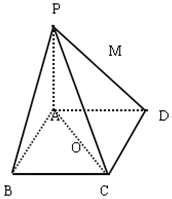 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥面ABCD,PA=AD=4,AB=2,以AC中点O为球心,AC为直径的球面交线段PD(不含端点)于M.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥面ABCD,PA=AD=4,AB=2,以AC中点O为球心,AC为直径的球面交线段PD(不含端点)于M.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
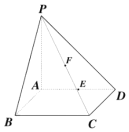 如图:在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是正方形,PA=AD=2.
如图:在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是正方形,PA=AD=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 项目 | 生产成本 | 检验费/次 | 调试费 | 出厂价 |
| 金额(元) | 1000 | 100 | 200 | 3000 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com