
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 根据存在t∈R,只要x∈[1,m],就有f(x+t)≤ex,即存在t∈[-2,0],满足${e^t}≤\frac{em}{e^m}$,令g(x)=ex-e3x,x∈[2,+∞),对g(x)进行求导,求其单调性,从而求出t的值,只要证明f(x-2)=e|x-2|≤ex对任意x∈[1,4]恒成立,即可.
解答 解:当x<0时,-x>0,则f(x)=f(-x)=e-x
综上:$f(x)=\left\{\begin{array}{l}{e^x},x≥0\\{e^{-x}},x<0\end{array}\right.$;
因为任意x∈[1,m],都有f(x+t)≤ex,
故f(1+t)≤e且f(m+t)≤em,
当1+t≥0时,e1+t≤e,从而1+t≤1,
∴-1≤t≤0
当1+t<0时,e-(1+t)≤e,从而-(1+t)≤1,
∴-2≤t<-1
综上-2≤t≤0∵m≥2,故m+t>0
故f(m+t)≤em得:em+t≤em
即存在t∈[-2,0],满足${e^t}≤\frac{em}{e^m}$
∴$\frac{em}{e^m}≥{\{{e^t}\}_{min}}={e^{-2}}$,即em-e3m≤0
令g(x)=ex-e3x,x∈[2,+∞),则g′(x)=ex-e3
当x∈(2,3)时,g'(x)<0,g(x)单调递减
当x∈(3,+∞)时,g'(x)>0,g(x)单调递增
又g(3)=-2e3<0,g(2)=-e3<0,g(4)=e3(e-4)<0,g(5)=e3(e2-4)>0
由此可见,方程g(x)=0在区间[2,+∞)上有唯一解m0∈(4,5),
且当x∈[2,m0]时g(x)≤0,当x∈[m0,+∞)时g(x)≥0
∵m∈Z,故mmax=4,此时t=-2,
故选:C
点评 此题主要考查利用导数研究函数的单调性以及偶函数的性质,解题的过程中用到了分类讨论和转化的思想,有一定的难度.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | [0,$\frac{1}{2}$) | B. | (-$\frac{1}{2}$,1] | C. | [-1,$\frac{1}{2}$) | D. | (-$\frac{1}{2}$,0] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
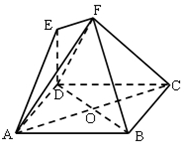 如图,多面体EF-ABCD中,四边形ABCD是菱形,AB=4,∠BAD=60°,AC,BD相交于O,EF∥AC,点E在平面ABCD上的射影恰好是线段AO的中点.
如图,多面体EF-ABCD中,四边形ABCD是菱形,AB=4,∠BAD=60°,AC,BD相交于O,EF∥AC,点E在平面ABCD上的射影恰好是线段AO的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向右平移$\frac{π}{2}$个单位 | B. | 向右平移$\frac{π}{4}$个单位 | ||
| C. | 向左平移$\frac{π}{2}$个单位 | D. | 向左平移$\frac{π}{4}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2016) | B. | (-2018,-2016) | ||
| C. | (-2018,+∞) | D. | (-∞,-2018)∪(-2016,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{9}$ | C. | 3 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在一段直行的公路上方D处有一测速球机,在球机下方路面有A,B,C三个测速点,测得球机距点A为14米,AB=10米,球机探测点B和C的俯角分别为60°和45°,现有一小汽车从A地到C地用时1秒,则小汽车经过AC这段路程的平均速度约为18.1米/秒.(结果精确到0.1,参考数据$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)
如图,在一段直行的公路上方D处有一测速球机,在球机下方路面有A,B,C三个测速点,测得球机距点A为14米,AB=10米,球机探测点B和C的俯角分别为60°和45°,现有一小汽车从A地到C地用时1秒,则小汽车经过AC这段路程的平均速度约为18.1米/秒.(结果精确到0.1,参考数据$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com