
分析 (Ⅰ)n=6时,利用n次独立重复试验中事件A恰好发生k次的概率计算公式能求出恰有4件产品通过质量检测的概率.
(Ⅱ)当X=S5时,X的可能取值为-50,-30,-10,10,30,50,分别求出相应的概率,由此能求出X的分布列和EX.
解答 解:(Ⅰ)n=6时,恰有4件产品通过质量检测的概率:
P=${C}_{6}^{4}(\frac{2}{3})^{4}(\frac{1}{3})^{2}$=$\frac{80}{243}$.
(Ⅱ)∵X=S5,∴X的可能取值为-50,-30,-10,10,30,50,
P(X=-50)=${C}_{5}^{0}(\frac{1}{3})^{5}$=$\frac{1}{243}$,
P(X=-30)=${C}_{5}^{1}(\frac{2}{3})(\frac{1}{3})^{4}$=$\frac{10}{243}$,
P(X=-10)=${C}_{5}^{2}(\frac{2}{3})^{2}(\frac{1}{3})^{3}$=$\frac{40}{243}$,
P(X=10)=${C}_{5}^{3}(\frac{2}{3})^{3}(\frac{1}{3})^{2}$=$\frac{80}{243}$,
P(X=30)=${C}_{5}^{4}(\frac{2}{3})^{4}(\frac{1}{3})$=$\frac{80}{243}$,
P(X=50)=${C}_{5}^{5}(\frac{2}{3})^{5}$=$\frac{32}{243}$,
∴X的分布列为:
| X | -50 | -30 | -10 | 10 | 30 | 50 |
| P | $\frac{1}{243}$ | $\frac{10}{243}$ | $\frac{40}{243}$ | $\frac{80}{243}$ | $\frac{80}{243}$ | $\frac{32}{243}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列及数学期望的求法及应用,考查推理论证能力、运算求解能力,考查函数与方程思想、化归转化思想,是中档题.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:选择题
| A. | 奇函数,且在(0,e)上是增函数 | B. | 奇函数,且在(0,e)上是减函数 | ||
| C. | 偶函数,且在(0,e)上是增函数 | D. | 偶函数,且在(0,e)上是减函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,$\frac{1}{2}$) | B. | (-$\frac{1}{2}$,1] | C. | [-1,$\frac{1}{2}$) | D. | (-$\frac{1}{2}$,0] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a$≤\frac{1}{15}$ | B. | a<$\frac{1}{15}$ | C. | a$≥\frac{1}{15}$ | D. | a>$\frac{1}{15}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{5}-1$ | B. | $2\sqrt{5}$ | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
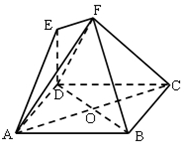 如图,多面体EF-ABCD中,四边形ABCD是菱形,AB=4,∠BAD=60°,AC,BD相交于O,EF∥AC,点E在平面ABCD上的射影恰好是线段AO的中点.
如图,多面体EF-ABCD中,四边形ABCD是菱形,AB=4,∠BAD=60°,AC,BD相交于O,EF∥AC,点E在平面ABCD上的射影恰好是线段AO的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2016) | B. | (-2018,-2016) | ||
| C. | (-2018,+∞) | D. | (-∞,-2018)∪(-2016,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com