
【题目】已知△ABC的内角A,B,C的对边分别为a,b,c,且asinB=bsin(A+![]() ).
).
(1)求A;
(2)若b,![]() a,c成等差数列,△ABC的面积为2
a,c成等差数列,△ABC的面积为2![]() ,求a.
,求a.
【答案】(1)![]() ; (2)
; (2)![]() .
.
【解析】
(1)由正弦定理化简已知可得sinA=sin(A+![]() ),结合范围A∈(0,π),即可计算求解A的值;
),结合范围A∈(0,π),即可计算求解A的值;
(2)利用等差数列的性质可得b+c=![]() ,利用三角形面积公式可求bc的值,进而根据余弦定理即可解得a的值.
,利用三角形面积公式可求bc的值,进而根据余弦定理即可解得a的值.
(1)∵asinB=bsin(A+![]() ).
).
∴由正弦定理可得:sinAsinB=sinBsin(A+![]() ).
).
∵sinB≠0,
∴sinA=sin(A+![]() ).
).
∵A∈(0,π),可得:A+A+![]() =π,
=π,
∴A=![]() .
.
(2)∵b,![]() a,c成等差数列,
a,c成等差数列,
∴b+c=![]() ,
,
∵△ABC的面积为2![]() ,可得:S△ABC=
,可得:S△ABC=![]() bcsinA=2
bcsinA=2![]() ,
,
∴![]() =2
=2![]() ,解得bc=8,
,解得bc=8,
∴由余弦定理可得:a2=b2+c2﹣2bccosA=(b+c)2﹣2bc﹣2bccos![]()
=(b+c)2﹣3bc=(![]() a)2﹣24,
a)2﹣24,
∴解得:a=2![]() .
.


 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为F.
的右焦点为F.
(1)求点F的坐标和椭圆C的离心率;
(2)直线![]() 过点F,且与椭圆C交于P,Q两点,如果点P关于x轴的对称点为
过点F,且与椭圆C交于P,Q两点,如果点P关于x轴的对称点为![]() ,判断直线
,判断直线![]() 是否经过x轴上的定点,如果经过,求出该定点坐标;如果不经过,说明理由.
是否经过x轴上的定点,如果经过,求出该定点坐标;如果不经过,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面的茎叶图记录了甲、乙两代表队各10名同学在一次英语听力比赛中的成绩(单位:分).已知甲代表队数据的中位数为76,乙代表队数据的平均数是75.

(1)求![]() ,
,![]() 的值;
的值;
(2)若分别从甲、乙两队随机各抽取1名成绩不低于80分的学生,求抽到的学生中,甲队学生成绩不低于乙队学生成绩的概率;
(3)判断甲、乙两队谁的成绩更稳定,并说明理由(方差较小者稳定).
查看答案和解析>>
科目:高中数学 来源: 题型:
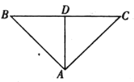
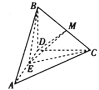
【题目】如图,将斜边长为![]() 的等腰直角
的等腰直角![]() 沿斜边
沿斜边![]() 上的高
上的高![]() 折成直二面角
折成直二面角![]() ,
,![]() 为
为![]() 中点.
中点.
(1)求二面角![]() 的余弦值;
的余弦值;
(2)![]() 为线段
为线段![]() 上一动点,当直线
上一动点,当直线![]() 与平面
与平面![]() 所成的角最大时,求三棱锥
所成的角最大时,求三棱锥![]() 外接球的体积.
外接球的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】动圆![]() 过定点
过定点![]() ,且在
,且在![]() 轴上截得的弦
轴上截得的弦![]() 的长为4.
的长为4.
(1)若动圆圆心![]() 的轨迹为曲线
的轨迹为曲线![]() ,求曲线
,求曲线![]() 的方程;
的方程;
(2)在曲线![]() 的对称轴上是否存在点
的对称轴上是否存在点![]() ,使过点
,使过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 的交点
的交点![]() 满足
满足![]() 为定值?若存在,求出点
为定值?若存在,求出点![]() 的坐标及定值;若不存在,请说明理由.
的坐标及定值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是自然对数的底数,函数
是自然对数的底数,函数![]() 与
与![]() 的定义域都是
的定义域都是![]() .
.
(1)求函数![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)判断函数![]() 零点个数;
零点个数;
(3)用![]() 表示
表示![]() 的最小值,设
的最小值,设![]() ,
,![]() ,若函数
,若函数![]() 在
在![]() 上为增函数,求实数
上为增函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com