
【题目】BMI指数(身体质量指数,英文为BodyMassIndex,简称BMI)是衡量人体胖瘦程度的一个标准,BMI=体重(kg)/身高(m)的平方.根据中国肥胖问题工作组标准,当BMI≥28时为肥胖.某地区随机调查了1200名35岁以上成人的身体健康状况,其中有200名高血压患者,被调查者的频率分布直方图如下:
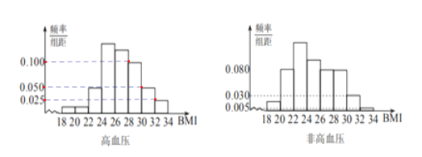
(1)求被调查者中肥胖人群的BMI平均值![]() ;
;
(2)填写下面列联表,并判断是否有99.9%的把握认为35岁以上成人患高血压与肥胖有关.
| 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
肥胖 | 不肥胖 | 合计 | |
高血压 | |||
非高血压 | |||
合计 |
附: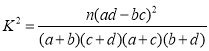 ,
,![]()
【答案】(1)![]() (2)填表见解析;有99.9%的把握认为35岁以上成人患高血压与肥胖有关
(2)填表见解析;有99.9%的把握认为35岁以上成人患高血压与肥胖有关
【解析】
(1)分别计算高血压和非高血压人群中各BMI值段的人数,然后用各BMI值段的人数乘以频率分布直方图每个对应表格的中点再求和,最后除以总人数则可得到平均值. (2)根据频率分布直方图,分别计算高血压人群、非高血压人群中肥胖和不肥胖的人数,填表,然后计算观测值![]() ,对应给出的表格,得出结论.
,对应给出的表格,得出结论.
解:(1)根据频率分布直方图,200名高血压患者中,BMI值在![]() 的人数为
的人数为![]() ,在
,在![]() 的人数为
的人数为![]() ,在
,在![]() 的人数为
的人数为![]()
1000名非高血压患者中,BMI值在![]() 的人数为
的人数为![]() ,在
,在![]() 的人数为
的人数为![]() ,在
,在![]() 的人数为
的人数为![]()
被调查者中肥胖人群的BMI平均值![]()
(2)由(1)知,200名高血压患者中,有![]() 人肥胖,
人肥胖,![]() 人不肥胖
人不肥胖
1000名非高血压患者中,有![]() 人肥胖,
人肥胖,![]() 人不肥胖
人不肥胖
肥胖 | 不肥胖 | 合计 | |
高血压 | 70 | 130 | 200 |
非高血压 | 230 | 770 | 1000 |
合计 | 300 | 900 | 1200 |
![]()
有99.9%的把握认为35岁以上成人患高血压与肥胖有关.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】若n是一个三位正整数,且n的个位数字大于十位数字,十位数字大于百位数字,则称n为“三位递增数”(如137,359,567等).
在某次数学趣味活动中,每位参加者需从所有的“三位递增数”中随机抽取1个数,且只能抽取一次.得分规则如下:若抽取的“三位递增数”的三个数字之积不能被5整除,参加者得0分;若能被5整除,但不能被10整除,得-1分;若能被10整除,得1分.
(1)写出所有个位数字是5的“三位递增数”;
(2)若甲参加活动,求甲得分X的分布列和数学期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若函数![]() 在其定义域内单调递增,求实数
在其定义域内单调递增,求实数![]() 的取值范围;
的取值范围;
(2)是否存在实数![]() ,使得函数
,使得函数![]() 的图象与
的图象与![]() 轴相切?若存在,求满足条件的
轴相切?若存在,求满足条件的![]() 的取值范围,请说明理由.
的取值范围,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将正方形![]() 沿对角线
沿对角线![]() 折成直二面角
折成直二面角![]() ,有如下四个结论:
,有如下四个结论:
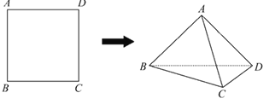
(1)![]() ;(2)
;(2)![]() 是等边三角形;
是等边三角形;
(3)![]() 与平面
与平面![]() 所成的角为60°;(4)
所成的角为60°;(4)![]() 与
与![]() 所成的角为
所成的角为![]() .
.
其中错误的结论是( )
A.(1)B.(2)C.(3)D.(4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为抛物线
为抛物线![]() 上的一点,
上的一点,![]() ,
,![]() 为抛物线上异于点
为抛物线上异于点![]() 的两点,且直线
的两点,且直线![]() 的斜率与直线
的斜率与直线![]() 的斜率互为相反数.
的斜率互为相反数.
(1)求直线![]() 的斜率;
的斜率;
(2)设直线![]() 过点
过点![]() 并交抛物线于
并交抛物线于![]() ,
,![]() 两点,且
两点,且![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,试探究
,试探究![]() 与
与![]() 的夹角是否为定值,若是则求出定值,若不是,说明理由.
的夹角是否为定值,若是则求出定值,若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】算盘是中国传统的计算工具,其形长方,周为木框,内贯直柱,俗称“档”,档中横以梁,梁上两珠,每珠作数五,梁下五珠,每珠作数一.算珠梁上部分叫上珠,梁下部分叫下珠.例如:在十位档拨上一颗上珠和一颗下珠,个位档拨上一颗上珠,则表示数字65.若在个、十、百、千位档中随机选择一档拨一颗上珠,再随机选择两个档位各拨一颗下珠,则所拨数字大于200的概率为( ).

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有边长均为1的正方形正五边形正六边形及半径为1的圆各一个,在水平桌面上无滑动滚动一周,它们的中心的运动轨迹长分别为![]() ,
,![]() ,
,![]() ,
,![]() ,则( )
,则( )
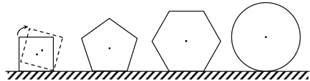
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两个分类变量X和Y,由他们的观测数据计算得到K2的观测值范围是3.841<k<6.635,据K2的临界值表,则以下判断正确的是( )
![]()
P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
A.在犯错误概率不超过0.05的前提下,认为变量X与Y有关系
B.在犯错误概率不超过0.05的前提下,认为变量X与Y没有关系
C.在犯错误概率不超过0.01的前提下,认为变量X与Y有关系
D.在犯错误概率不超过0.01的前提下,认为变量X与Y没有关系
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某公司举行的一次真假游戏的有奖竞猜中,设置了“科技”和“生活”这两类试题,规定每位职工最多竞猜3次,每次竞猜的结果相互独立.猜中一道“科技”类试题得4分,猜中一道“生活”类试题得2分,两类试题猜不中的都得0分.将职工得分逐次累加并用X表示,如果X的值不低于4分就认为通过游戏的竞猜,立即停止竞猜,否则继续竞猜,直到竞猜完3次为止.竞猜的方案有以下两种:方案1:先猜一道“科技”类试题,然后再连猜两道“生活”类试题;
方案2:连猜三道“生活”类试题.
设职工甲猜中一道“科技”类试题的概率为0.5,猜中一道“生活”类试题的概率为0.6.
(1)你认为职工甲选择哪种方案通过竞猜的可能性大?并说明理由.
(2)职工甲选择哪一种方案所得平均分高?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com