已知函数f(x)=x2-2ax+5(a>1).
(1)若f(x)的定义域和值域均是[1,a],求实数a的值;
(2)若f(x)在区间(-∞,2]上是减函数,且对任意的x1,x2∈[1,1+a],总有|f(x1)-f(x2)|≤9,求实数a的取值范围.
解:(1)∵f(x)=(x-a)
2+5-a
2(a>1),
∴y=f(x)在[1,a]上是减函数,…(2分)
又定义域和值域均为[1,a],∴

,…(4分)
即
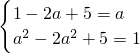
,解得 a=2. …(6分)
(2)∵f(x)在区间(-∞,2]上是减函数,∴a≥2,…(7分)
又对称轴为x=a,a∈[1,a+1],且(a+1)-a≤a-1
∴f(x)
max=f(1)=6-2a,f(x)
min=f(a)=5-a
2. …(10分)
∵对任意的x
1,x
2∈[1,a+1],总有|f(x
1)-f(x
2)|≤9,
∴f(x)
max-f(x)
min≤9,
即 (6-2a)-(5-a
2)≤9,解得-2≤a≤4,…(13分)
又a≥2,∴2≤a≤4. …(14分)
分析:(1)先将函数进行配方得到对称轴,判定出函数f(x)在[1,a]上的单调性,然后根据定义域和值域均为[1,a]建立方程组,解之即可;
(2)将a与2进行比较,将条件“对任意的x
1,x
2∈[1,1+a],总有|f(x
1)-f(x
2)|≤9”转化成“对任意的x
1,x
2∈[1,1+a],总有f(x)
max-f(x)
min≤9恒成立”即可.
点评:本题考查的知识点是二次函数在闭区间上的最值,二次函数的性质,其中(1)的关键是判断出函数f(x)在[1,a]上的单调性,进而根据已知构造关于a的方程组,(2)的关键将“对任意的x
1,x
2∈[1,1+a],总有|f(x
1)-f(x
2)|≤9”转化成“对任意的x
1,x
2∈[1,1+a],总有f(x)
max-f(x)
min≤9恒成立“

 ,…(4分)
,…(4分)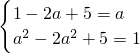 ,解得 a=2. …(6分)
,解得 a=2. …(6分)

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<