练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】从某小区抽取100户居民进行月用电量调查，发现其用电量都在50至350度之间，频率分布直方图如图所示，在这些用户中，用电量落在区间[150，250）内的户数为 ．

    【答案】52
    【解析】解：由用电量落在区间[150，250）内频率为：
    1﹣（0.0024+0.0036+0.0024+0.0012）×50=0.52，
    ∴用电量落在区间[150，250）内的户数为：
    100×0.52=52．
    所以答案是：52．
    【考点精析】通过灵活运用频率分布直方图，掌握频率分布表和频率分布直方图，是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式，可展示数据的分布情况.通过作图既可以从数据中提取信息，又可以利用图形传递信息即可以解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，曲线C1的参数方程为： （α为参数），以原点为极点，x轴的正半轴为极轴，并取与直角坐标系相同的长度单位，建立极坐标系，曲线C2的极坐标方程为：ρ=cosθ． （Ⅰ）求曲线C2的直角坐标方程；
    （Ⅱ）若P，Q分别是曲线C1和C2上的任意一点，求|PQ|的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点A（2sinx，﹣cosx）、B（ cosx，2cosx），记f（x）= ．
    （1）若x0是函数y=f（x）﹣1的零点，求tanx0的值；
    （2）求f（x）在区间[ ， ]上的最值及对应的x的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在一次耐力和体能测试之后，某校对其甲、乙、丙、丁四位学生的耐力成绩（）和体能成绩（）进行回归分析，求得回归直线方程为．由于某种原因，成绩表（如下表所示）中缺失了乙的耐力和体能成绩．

    甲

    乙

    丙

    丁

    耐力成绩(X)

    7.5

    m

    8

    8.5

    体能成绩(Y)

    8

    n

    8.5

    9.5

    综合素质

    （）

    15.5

    16

    16.5

    18

    （Ⅰ）请设法还原乙的耐力成绩和体能成绩；

    （Ⅱ）在区域性校际学生身体综合素质比赛中，由甲、乙、丙、丁四位学生组成学校代表队参赛.共举行3场比赛，每场比赛均由赛事主办方从学校代表中随机抽两人参赛，每场比赛所抽的选手中，只要有一名选手的综合素质分高于16分，就能为所在学校赢得一枚荣誉奖章．若记比赛中赢得荣誉奖章的枚数为，试根据上表所提供数据，预测该校所获奖章数的分布列与数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=cosωx（sinωx+ cosωx）（ω＞0），如果存在实数x0 ， 使得对任意的实数x，都有f（x0）≤f（x）≤f（x0+2016π）成立，则ω的最小值为（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数f（x）= x2+ax﹣lnx（a∈R）．
    （1）当a=1时，求函数f（x）的极值；
    （2）当a＞1时，讨论函数f（x）的单调性；
    （3）若对任意a∈（3，4）及任意x1 ， x2∈[1，2]，恒有 m+ln2＞|f（x1）﹣f（x2）|成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知某单位有50名职工，现要从中抽取 10名职工，将全体职工随机按1~50编号，并按编号顺序平均分成10组，按各组内抽取的编号依次增加5进行系统抽样．

    （Ⅰ）若第5组抽出的号码为22，写出所有被抽出职工的号码；

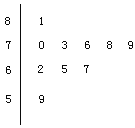
    （Ⅱ）分别统计这10名职工的体重（单位：公斤），获得体重数据的茎叶图如图所示，求该样本的平均数、中位数和方差；

    （Ⅲ）在（Ⅱ）的条件下，从这10名职工中随机抽取两名体重不轻于73公斤（73公斤）的职工，求体重为81公斤的职工被抽取到的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】甲、乙、丙、丁四个物体同时从某一点出发向同一个方向运动，其路程fi（x）（i=1，2，3，4）关于时间x（x≥0）的函数关系式分别为f1（x）=2x﹣1，f2（x）=x3 ， f3（x）=x，f4（x）=log2（x+1），有以下结论：
    ①当x＞1时，甲走在最前面；
    ②当x＞1时，乙走在最前面；
    ③当0＜x＜1时，丁走在最前面，当x＞1时，丁走在最前面；
    ④丙不可能走在最前面，也不可能走在最后面；
    ⑤如果它们一直运动下去，最终走在最前面的是甲．
    其中，正确结论的序号为（把正确结论的序号都填上，多填或少填均不得分）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知椭圆C1： +y2=1，双曲线C2： =1（a＞0，b＞0），若以C1的长轴为直径的圆与C2的一条渐近线交于A，B两点，且C1与该渐近线的两交点将线段AB三等分，则C2的离心率为（ ）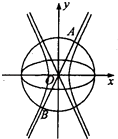
    A.
    B.5
    C.
    D.

    查看答案和解析>>

    同步练习册答案