Question

知
（1）求sinβ；
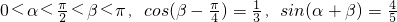
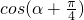（2）求sin2β的值；
（3）求的值．

Answer 1

解：（1）∵，∴=，
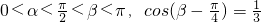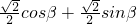∴cosβ+sinβ=，又 cos²β+sin²β=1，解得sinβ=．
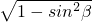（2）由（1）知，cosβ=-=-，∴sin2β=2sinβcosβ=-．
（3）由已知条件可得 β-为锐角，α+β为钝角，∴sin（β-）=，cos（α+β）=-，
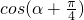∴=cos[（α+β）-（ β-）]=cos（α+β）•cos（ β-）+sin（α+β）•sin（ β-）
=-•+•=．
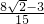分析：（1）由条件可得 cosβ+sinβ=，再根据 cos²β+sin²β=1 求出sinβ的值．
（2） 先根据同角三角函数的基本关系求出cosβ 值，用二倍角公式可求sin2β．
（3）根据角的范围求出sin（β-）和cos（α+β），由 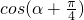=cos[（α+β）-（ β-）]运算化简得出结果．
点评：本题考查同角三角函数的基本关系，两角和差的三角公式，二倍角公式的应用，角的变换和角的范围的确定是解题的难点．