
已知函数
 为自然对数的底数).
为自然对数的底数).
(1)求曲线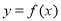 在
在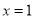 处的切线方程;
处的切线方程;
(2)若 是
是 的一个极值点,且点
的一个极值点,且点 ,
, 满足条件:
满足条件: .
.
(ⅰ)求 的值;
的值;
(ⅱ)若点 是三个不同的点, 判断
是三个不同的点, 判断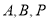 三点是否可以构成直角三
三点是否可以构成直角三
角形?请说明理由。
(1) ;(2)
;(2) ;点
;点 ,
, ,
, 可构成直角三角形.
可构成直角三角形.
【解析】
试题分析:本题主要考查导数的运算、利用导数求曲线的切线方程、利用导数判断函数的单调性、利用导数求函数的最值和极值、向量垂直的充要条件等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力.第一问,对 求导,将切点的横坐标1代入到
求导,将切点的横坐标1代入到 中得到切线的斜率,代入到
中得到切线的斜率,代入到 中得到切点的纵坐标,从而利用点斜式得到切线方程;第二问,先求函数的定义域,令
中得到切点的纵坐标,从而利用点斜式得到切线方程;第二问,先求函数的定义域,令 ,得到方程的根,将定义域断开,判断函数的单调性,从而求出函数极值;第三问,先排除几个特例情况,在一般情况中,要证明三角形为直角三角形,只需判断2边垂直,用向量垂直的充要条件证明即可.
,得到方程的根,将定义域断开,判断函数的单调性,从而求出函数极值;第三问,先排除几个特例情况,在一般情况中,要证明三角形为直角三角形,只需判断2边垂直,用向量垂直的充要条件证明即可.
试题解析:(1) ,
,  ,又
,又 ,所以曲线
,所以曲线 在
在 处的切线方程为
处的切线方程为 ,即
,即 .
.
(2)(ⅰ)对于 ,定义域为
,定义域为 .
.
当 时,
时, ,
, ,∴
,∴ ;
;
当 时,
时, ;当
;当 时,
时, ,
, ,∴
,∴
所以 存在唯一的极值点
存在唯一的极值点 ,∴
,∴ ,则点
,则点 为
为
(ⅱ)若 ,则
,则 ,与条件
,与条件 不符,
不符,
从而得 .同理可得
.同理可得 .
.
若 ,则
,则 ,与条件
,与条件 不符,从而得
不符,从而得 .
.
由上可得点 ,
, ,
, 两两不重合.
两两不重合.




从而 ,点
,点 ,
, ,
, 可构成直角三角形.
可构成直角三角形.
考点:导数的运算、利用导数求曲线的切线方程、利用导数判断函数的单调性、利用导数求函数的最值和极值、向量垂直的充要条件.


科目:高中数学 来源:2013-2014学年福建省福州市高三5月综合练习文科数学试卷(解析版) 题型:选择题
某公司的一品牌电子产品,2013年年初,由于市场疲软,产品销售量逐渐下降,五月份公司加大了宣传力度,销售量出现明显的回升,九月份,公司借大学生开学之际,采取了促销等手段,产品的销售量猛增,十一月份之后,销售量有所回落.下面大致能反映出公司2013年该产品销售量的变化情况的图象是( )

查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省高考考前模拟文科数学试卷(解析版) 题型:解答题
为了解某校学生的视力情况,现采用随机抽样的方式从该校的A,B两班中各抽5名学生进行视力检测.检测的数据如下:
A班5名学生的视力检测结果:4.3,5.1,4.6,4.1,4.9.
B班5名学生的视力检测结果:5.1,4.9,4.0,4.0,4.5.
(1)分别计算两组数据的平均数,从计算结果看,哪个班的学生视力较好?;
(2)由数据判断哪个班的5名学生视力方差较大?(结论不要求证明)
(3)根据数据推断A班全班40名学生中有几名学生的视力大于4.6?
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省高考考前模拟文科数学试卷(解析版) 题型:选择题
已知曲线 :
: 和
和 :
: 的焦点分别为
的焦点分别为 、
、 ,点
,点 是
是 和
和 的一个交点,则△
的一个交点,则△ 的形状是( )
的形状是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.都有可能
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省漳州市毕业班质量检查理科数学试卷(解析版) 题型:选择题
已知正三角形ABC的顶点A(1,1),B(1,3),顶点C在第一象限,若点(x,y)在△ABC内部,则z=-x+y的取值范围是
A.(1-,2) B.(0,2) C.(-1,2) D.(0,1+)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com