
 的取值范围;
的取值范围;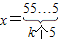 时,都有
时,都有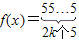 成立,则称这样f(x)是K2函数,现有函数
成立,则称这样f(x)是K2函数,现有函数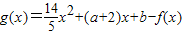 ,试判断g(x)是不是K2函数?并给予证明.?
,试判断g(x)是不是K2函数?并给予证明.?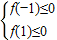 得到
得到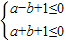 ,再观察
,再观察 的结构形式,可用线性规划解决;
的结构形式,可用线性规划解决;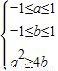 ,可用定积分求得有零点时的面积,从而求得有零 点时的概率,再用对立事件求得无零点时的概率;
,可用定积分求得有零点时的面积,从而求得有零 点时的概率,再用对立事件求得无零点时的概率;  ∴
∴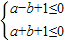
 的几何意义是定点P(2,5)到区域内的点Q(a,b)连线的斜率k,
的几何意义是定点P(2,5)到区域内的点Q(a,b)连线的斜率k,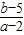 的取值范围为(-∞,-1)∪(1,+∞);
的取值范围为(-∞,-1)∪(1,+∞);
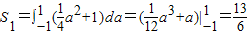 ,
,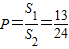 ,∴f(x)无零点的概率为
,∴f(x)无零点的概率为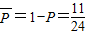 ;
;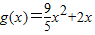 符合条件,
符合条件,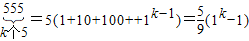 ,
, ;
;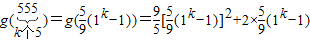
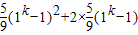 =
=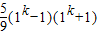 =
=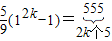 ,
, 符合条件.
符合条件.

科目:高中数学 来源: 题型:
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 3 |
| f′(x) |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x |
| a |
| b |
| x |
| 4c2 |
| k(k+c) |
查看答案和解析>>
科目:高中数学 来源:上海模拟 题型:解答题
| x |
| a |
| b |
| x |
| 4c2 |
| k(k+c) |
查看答案和解析>>
科目:高中数学 来源:深圳一模 题型:解答题
| 1 |
| 3 |
| f′(x) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com