
| A. | 16 | B. | 17 | C. | 14 | D. | 15 |
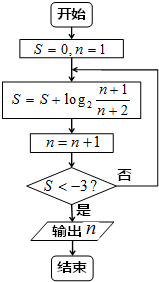
分析 通过分析循环,推出循环规律,利用循环的次数,求出输出结果.
解答 解:第一次循环:S=log2$\frac{2}{3}$,n=2;
第二次循环:S=log2$\frac{2}{3}$+log2$\frac{3}{4}$,n=3;
第三次循环:S=log2$\frac{2}{3}$+log2$\frac{3}{4}$+log2$\frac{4}{5}$,n=4;
…
第n次循环:S=log2$\frac{2}{3}$+log2$\frac{3}{4}$+log2$\frac{4}{5}$+…+log2$\frac{n}{n+1}$=log2$\frac{2}{n+2}$,n=n+1;
令log2$\frac{2}{n+2}$<-3,解得n>13.
∴输出的结果是n+1=14.
故选:C.
点评 本题考查程序框图的应用,数列的应用,考查分析问题解决问题的能力,属于基础题.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4 | B. | 4或$-\frac{17}{2}$ | C. | -4或4 | D. | -4或4或-$\frac{17}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{\sqrt{2}}{8}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2014 | B. | 2015 | C. | 2016 | D. | 2017 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
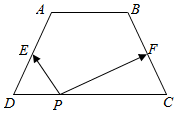 如图,在等腰梯形ABCD中,AB=2,CD=4,BC=$\sqrt{5}$,点E,F分别为AD,BC的中点.如果对于常数λ,在ABCD的四条边上,有且只有8个不同的点P使得$\overrightarrow{PE}$•$\overrightarrow{PF}$=λ成立,那么实数λ的取值范围为(-$\frac{9}{20}$,-$\frac{1}{4}$).
如图,在等腰梯形ABCD中,AB=2,CD=4,BC=$\sqrt{5}$,点E,F分别为AD,BC的中点.如果对于常数λ,在ABCD的四条边上,有且只有8个不同的点P使得$\overrightarrow{PE}$•$\overrightarrow{PF}$=λ成立,那么实数λ的取值范围为(-$\frac{9}{20}$,-$\frac{1}{4}$).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com