
【题目】定义平面向量之间的一种运算“⊙”如下:对任意的 ![]() ,令
,令 ![]() ,下面说法错误的是( )
,下面说法错误的是( )
A.若 ![]() 与
与 ![]() 共线,则
共线,则 ![]() ⊙
⊙ ![]() =0
=0
B.![]() ⊙
⊙ ![]() =
= ![]() ⊙
⊙ ![]()
C.对任意的λ∈R,有 ![]() ⊙
⊙ ![]() =
= ![]() ⊙
⊙ ![]() )
)
D.( ![]() ⊙
⊙ ![]() )2+(
)2+( ![]() )2=|
)2=| ![]() |2|
|2| ![]() |2
|2
【答案】B
【解析】解:对于A,若 ![]() 与
与 ![]() 共线,则有
共线,则有 ![]() ,故A正确; 对于B,因为
,故A正确; 对于B,因为 ![]() ,而
,而 ![]() ,所以有
,所以有 ![]() ,故选项B错误,
,故选项B错误,
对于C, ![]() ⊙
⊙ ![]() =λqm﹣λpn,而
=λqm﹣λpn,而 ![]() ⊙
⊙ ![]() )=λ(qm﹣pn)=λqm﹣λpn,故C正确,
)=λ(qm﹣pn)=λqm﹣λpn,故C正确,
对于D,( ![]() ⊙
⊙ ![]() )2+(
)2+( ![]() )2=(qm﹣pn)2+(mp+nq)2=(m2+n2)(p2+q2)=|
)2=(qm﹣pn)2+(mp+nq)2=(m2+n2)(p2+q2)=| ![]() |2|
|2| ![]() |2 , D正确;
|2 , D正确;
故选B.
根据题意对选项逐一分析.若 ![]() 与
与 ![]() 共线,则有
共线,则有 ![]() ,故A正确;
,故A正确;
因为 ![]() ,而
,而 ![]() ,所以有
,所以有 ![]() ,故选项B错误,
,故选项B错误,
对于C, ![]() ⊙
⊙ ![]() =λqm﹣λpn,而
=λqm﹣λpn,而 ![]() ⊙
⊙ ![]() )=λ(qm﹣pn)=λqm﹣λpn,故C正确,
)=λ(qm﹣pn)=λqm﹣λpn,故C正确,
对于D,( ![]() ⊙
⊙ ![]() )2+(
)2+( ![]() )2=(qm﹣pn)2+(mp+nq)2=(m2+n2)(p2+q2)=|
)2=(qm﹣pn)2+(mp+nq)2=(m2+n2)(p2+q2)=| ![]() |2|
|2| ![]() |2 , D正确;
|2 , D正确;
得到答案.


科目:高中数学 来源: 题型:
【题目】近年来,福建省大力推进海峡西岸经济区建设,福州作为省会城市,在发展过程中,交通状况一直倍受有关部门的关注,据有关统计数据显示上午6点到10点,车辆通过福州市区二环路某一路段的用时y(分钟)与车辆进入该路段的时刻t之间关系可近似地用如下函数给出:y= 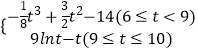 .求上午6点到10点,通过该路段用时最多的时刻.
.求上午6点到10点,通过该路段用时最多的时刻.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了增强高考与高中学习的关联度,考生总成绩由统一高考的语文、数学、外语3个科目成绩和高中学业水平考试3个科目成绩组成.保持统一高考的语文、数学、外语科目不变,分值不变,不分文理科,外语科目提供两次考试机会.计入总成绩的高中学业水平考试科目,由考生根据报考高校要求和自身特长,在思想政治、历史、地理、物理、化学、生物、信息技术七科目中自主选择三科.
(1)某高校某专业要求选考科目物理,考生若要报考该校该专业,则有多少种选考科目的选择;
(2)甲、乙、丙三名同学都选择了物理、化学、历史组合,各学科成绩达到二级的概率都是0.8,且三人约定如果达到二级不参加第二次考试,达不到二级参加第二次考试,如果设甲、乙、丙参加第二次考试的总次数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位建造一间背面靠墙的小房,地面面积为12m2 , 房屋正面每平方米造价为1200元,房屋侧面每平方米造价为800元,屋顶的造价为5800元,如果墙高为3m,且不计房屋背面和地面的费用,设房屋正面地面的边长为xm,房屋的总造价为y元.
(1)求y用x表示的函数关系式;
(2)怎样设计房屋能使总造价最低?最低总造价是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线过定点P(2,1).
(1)求经过点P且在两坐标轴上的截距相等的直线方程;
(2)若过点P的直线l与x轴和y轴的正半轴分别交于A,B两点,求△AOB面积的最小值及此时直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(2)令![]() ,区间
,区间 ,
, ![]() 为自然对数的底数。
为自然对数的底数。
(ⅰ)若函数![]() 在区间
在区间![]() 上有两个极值,求实数
上有两个极值,求实数![]() 的取值范围;
的取值范围;
(ⅱ)设函数![]() 在区间
在区间![]() 上的两个极值分别为
上的两个极值分别为![]() 和
和![]() ,
,
求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆C: ![]() 的左焦点为F,过点F的直线与椭圆C相交于A,B两点,直线l的倾斜角为60°,
的左焦点为F,过点F的直线与椭圆C相交于A,B两点,直线l的倾斜角为60°, ![]() .
. 
(1)求椭圆C的离心率;
(2)如果|AB|= ![]() ,求椭圆C的方程.
,求椭圆C的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且Sn=n(n+1),
(1)求数列{an}的通项公式an
(2)数列{bn}的通项公式bn= ![]() ,求数列{bn}的前n项和为Tn .
,求数列{bn}的前n项和为Tn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com