Question

已知函数f（x）=e^x•g（x），其中g（x）=ax²-2x-2．
（1）若存在x∈R，使得g（x）＞0成立，求实数a的取值范围；
（2）求函数y=f（|sinx|）的值域．

Answer 1

分析：（1）先判断g（x）二次项的系数，判断是否为二次函数，再求函数的最值求出a，
（2）求出函数的导数，根据导数求函数的极值和最值，画出图表，便于观察，求出函数的极值．

解答：解：（1）存在x∈R，使得g（x）＞0，
即存在x∈R，使得ax²-2x-2＞0，
当a＞0时，满足要求；当a=0时，满足要求；
当a＜0时，△＞0，解得-

1

2

＜a＜0
综上得，a＞-

1

2

（4分）
（2）f（x）=e^x•g（x）=e^x•（ax²-2x-2）
∴f′（x）=（e^x）′•（ax²-2x-2）+e^x•（ax²-2x-2）′
=e^x•（ax²-2x-2）+e^x•（2ax-2）
=e^x•[ax²+（2a-2）x-4]
设|sinx|=t，（0≤t≤1），则转化为求函数y=f（t），（0≤t≤1）的值域．
当a=0时，f′（x）=-2e^x•（x+2）＜0，此时函数f（t）在[0，1]上为减函数，
∴函数f（t）的值域为[f（1），f（0）]，即[（a-4）e，-2]
当a＜0时，f′(x)=ex•[ax2+(2a-2)x-4]=a•ex•(x-

2

a

)(x+2)＜0
此时函数f（t）在[0，1]上为减函数，
∴函数f（t）的值域为[f（1），f（0）]，即[（a-4）e，-2]（6分）
当a＞0时，f′(x)=ex•[ax2+(2a-2)x-4]=a•ex•(x-

2

a

)(x+2)
令f′（x）=0，解得x=

2

a

或x=-2（舍）．
当x变化时，f（x）与f′（x）的变化情况如下表：

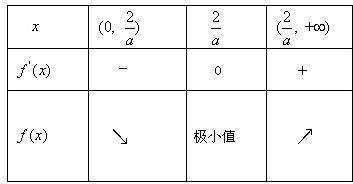
若

2

a

≥1，即0＜a≤2时，函数f（t）在[0，1]上为减函数．
∴函数f（t）的值域为[f（1），f（0）]，即[（a-4）e，-2]
若0＜

2

a

＜1，即a＞2时，函数f（t）在(0，

2

a

)上递减，在(

2

a

，1)上递增
∴ymin=f(

2

a

)=-2e

2

a

函数f（t）在[0，1]上的最大值为f（0）与f（1）中的较大者
∵f（0）=-2，f（1）=（a-4）e，∴f（1）-f（0）=（a-4）e+2
∴当a＞4-

2

e

时，f（1）＞f（0），此时y_max=f（1）=（a-4）e；
当a=4-

2

e

时，f（1）=f（0），此时y_max=f（0）=f（1）=-2；
当2＜a＜4-

2

e

时，f（1）＜f（0），此时y_max=f（0）=-2（13分）
综上，当a≤2时，函数f（|sinx|）的值域为[（a-4）e，-2]；
当2＜a≤4-

2

e

时，函数f（|sinx|）的值域为[-2e

2

a

，-2]；
当a＞4-

2

e

时，函数f（|sinx|）的值域为[-2e

2

a

，(a-4)e]．（14分）

点评：该题考查函数的求导，和g（x）是否为二次函数的判断，注意在解答过程中不要忘记画图，在解答过程中容易忽略判断二次项的系数，该地方是易错点．