
| A. | π | B. | 2π | C. | 4π | D. | $2\sqrt{5}π$ |
分析 首先,求解其内切球的半径,然后,结合球面的性质求解点O到平面DCN的距离,然后,确定其周长.
解答 解:根据题意,该正方体的内切球半径为r=$\sqrt{5}$,
由题意,取BB1的中点N,连接CN,则CN⊥BM,
∵正方体ABCD-A1B1C1D1,∴CN为DP在平面B1C1CB中的射影,
∴点P的轨迹为过D,C,N的平面与内切球的交线,
∵正方体ABCD-A1B1C1D1的棱长为2$\sqrt{5}$,
∴O到过D,C,N的平面的距离为1,
∴截面圆的半径为:$\sqrt{(\sqrt{5})^{2}-{1}^{2}}$=2,
∴点P的轨迹周长为:2π×2=4π.
故选:C.
点评 本题考查了正方体的性质、内切球的性质、线面位置关系与距离、勾股定理,考查了推理能力与计算能力,属于中档题.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:选择题
| A. | m=±2 | B. | m=2 | C. | m=-2 | D. | m≠±2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 全世界越来越关注环境保护问题,某省一监测站点于2016年8月某日起连续x天监测空气质量指数(AQI),数据统计如下:
全世界越来越关注环境保护问题,某省一监测站点于2016年8月某日起连续x天监测空气质量指数(AQI),数据统计如下:| 空气质量指数(μg/m3) | [0,50) | [50,100) | [100,150) | [150,200) | [201,250] |
| 空气质量等级 | 空气优 | 空气良 | 轻度污染 | 中度污染 | 重度污染 |
| 天数 | 20 | 40 | y | 10 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{4}-\frac{y^2}{16}=1$ | B. | $\frac{x^2}{16}-\frac{y^2}{4}=1$ | C. | $\frac{x^2}{16}-\frac{y^2}{64}=1$ | D. | $\frac{x^2}{64}-\frac{y^2}{16}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
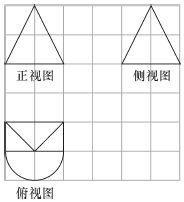 如图,网格纸上正方形的边长为1,图中粗实线画出的是一个几何体的三视图,则这个几何体的表面积是( )
如图,网格纸上正方形的边长为1,图中粗实线画出的是一个几何体的三视图,则这个几何体的表面积是( )| A. | $({1+\frac{{\sqrt{5}}}{2}})•π+2({1+\sqrt{5}})$ | B. | $\frac{{({1+\sqrt{5}})}}{2}•π+2({1+\sqrt{5}})$ | C. | $\frac{{({1+\sqrt{5}})}}{2}•π+2({3+\sqrt{5}})$ | D. | $\frac{{({1+\sqrt{5}})}}{2}•π+4+\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | a>c>b | C. | b>c>a | D. | c>b>a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com