
分析 (1)利用倍角公式、和差公式可得A,再利用同角三角函数基本关系式、正弦定理即可得出.
(2)由2sinB=sinC,利用正弦定理可得:2b=c,由余弦定理可得:a2=b2+c2-2bccosA,联立解出bc即可得出.
解答 解:(1)∵$\sqrt{3}sin2A+2{cos^2}A=2$,
∴$\sqrt{3}$sin2A+cos2A=1,
∴$\frac{\sqrt{3}}{2}$sin2A+$\frac{1}{2}$cos2A=$\frac{1}{2}$,
sin(2A+$\frac{π}{6}$)=$\frac{1}{2}$,∵A∈(0,π),
∴2A+$\frac{π}{6}$=$\frac{5π}{6}$,解得A=$\frac{π}{3}$.
由$cosB=\frac{{\sqrt{3}}}{3}$,B∈(0,π),∴sinB=$\sqrt{1-co{s}^{2}B}$=$\frac{\sqrt{6}}{3}$.
在△ABC中,由正弦定理可得:$\frac{a}{sinA}=\frac{b}{sinB}$,
可得b=$\frac{asinB}{sinA}$=$\frac{\sqrt{3}×\frac{\sqrt{6}}{3}}{\frac{\sqrt{3}}{2}}$=$\frac{2\sqrt{6}}{3}$.
(2)∵2sinB=sinC,∴2b=c,
由余弦定理可得:a2=b2+c2-2bccosA,
∴3=b2+c2-bc,与2b=c联立解得:b=1,c=2.
∴△ABC的面积S=$\frac{1}{2}bcsinA$=$\frac{1}{2}×1×2×\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$.
点评 本题考查了倍角公式、和差公式、正弦定理余弦定理、同角三角函数基本关系式、三角形面积计算公式,考查了推理能力与计算能力,属于中档题.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:解答题
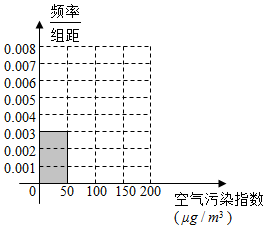 空气污染,又称为大气污染,是指由于人类活动或自然过程引起某些物质进入大气中,呈现出足够的浓度,达到足够的时间,并因此危害了人体的舒适、健康和福利或环境的现象.空气污染指数与空气质量级别和空气质量状况的关系如下表:
空气污染,又称为大气污染,是指由于人类活动或自然过程引起某些物质进入大气中,呈现出足够的浓度,达到足够的时间,并因此危害了人体的舒适、健康和福利或环境的现象.空气污染指数与空气质量级别和空气质量状况的关系如下表:| 空气污染指数 单位:μg/m3 | 0~50 | 50~100 | 100~150 | 150~200 | 200~300 | 300以上 |
| 空气质量级别 | 一级 | 二级 | 三级 | 四级 | 五级 | 六级 |
| 空气质量状况 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
| 空气污染指数 (单位:μg/m3) | [0,50] | (50,100] | (100,150] | (150,200] |
| 监测点个数 | 15 | 40 | y | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | [-2,2] | C. | [-∞,2] | D. | [0,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠BCD=120°,四边形BFED为矩形,平面BFED⊥平面ABCD,BF=1
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠BCD=120°,四边形BFED为矩形,平面BFED⊥平面ABCD,BF=1查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱柱ABCD-A1B1C1D1中,BB1⊥底面ABCD,AD∥BC,∠BAD=90°,AC⊥BD.
如图,在四棱柱ABCD-A1B1C1D1中,BB1⊥底面ABCD,AD∥BC,∠BAD=90°,AC⊥BD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com