
 空气污染,又称为大气污染,是指由于人类活动或自然过程引起某些物质进入大气中,呈现出足够的浓度,达到足够的时间,并因此危害了人体的舒适、健康和福利或环境的现象.空气污染指数与空气质量级别和空气质量状况的关系如下表:
空气污染,又称为大气污染,是指由于人类活动或自然过程引起某些物质进入大气中,呈现出足够的浓度,达到足够的时间,并因此危害了人体的舒适、健康和福利或环境的现象.空气污染指数与空气质量级别和空气质量状况的关系如下表:| 空气污染指数 单位:μg/m3 | 0~50 | 50~100 | 100~150 | 150~200 | 200~300 | 300以上 |
| 空气质量级别 | 一级 | 二级 | 三级 | 四级 | 五级 | 六级 |
| 空气质量状况 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
| 空气污染指数 (单位:μg/m3) | [0,50] | (50,100] | (100,150] | (150,200] |
| 监测点个数 | 15 | 40 | y | 10 |
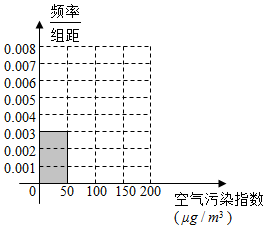
分析 (Ⅰ)根据频率分布直方图,利用频率=$\frac{频数}{样本容量}$,求出x、y的值,计算直方图中各小进行对应的高,补全频率分布直方图;
(Ⅱ)利用列举法求出基本事件数,计算对应的概率即可
解答 解:(Ⅰ)∵$0.003×50=\frac{15}{x}∴x=100$,
∵15+40+y+10=100,
∴y=35…(2分)
$\frac{40}{100×50}=0.008$,$\frac{35}{100×50}=0.007$,$\frac{10}{100×50}=0.002$,
故频率分布直方图如下图所示:
…(5分)
(Ⅱ)设A市空气质量状况属于轻度污染3个监测点为1,2,3,
空气质量状况属于良的2个监测点为4,5,
从中任取2个的基本事件分别为
(1,2),(1,3),(1,4),(1,5),(2,3),
(2,4),(2,5),(3,4),(3,5),(4,5)共10种,…(8分)
其中事件A“其中至少有一个为良”包含的 基本事件为
(1,4),(1,5),(2,4),(2,5),(3,4),(3,5),(4,5)共7种,…(10分)
所以事件A“其中至少有一个为良”发生的概率是$P(A)=\frac{7}{10}$.…(12分)
点评 本题考查了频率分布直方图的应用问题,也考查了用列举法求古典概型的概率问题,是基础题目


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 16 | C. | 9 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
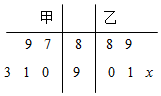 如图茎叶图记录了甲、乙两位射箭运动员的5次比赛成绩(单位:环),若两位运动员平均成绩相同,则成绩较为稳定(方差较小)的那位运动员成绩的方差为2.
如图茎叶图记录了甲、乙两位射箭运动员的5次比赛成绩(单位:环),若两位运动员平均成绩相同,则成绩较为稳定(方差较小)的那位运动员成绩的方差为2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某房地产公司新建小区有A、B两种户型住宅,其中A户型住宅每套面积为100平方米,B户型住宅每套面积为80平方米.该公司准备从两种户型住宅中各拿出12套销售给内部员工,表是这24套住宅每平方米的销售价格:(单位:万元/平方米):
某房地产公司新建小区有A、B两种户型住宅,其中A户型住宅每套面积为100平方米,B户型住宅每套面积为80平方米.该公司准备从两种户型住宅中各拿出12套销售给内部员工,表是这24套住宅每平方米的销售价格:(单位:万元/平方米):| 房号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| A户型 | 2.6 | 2.7 | 2.8 | 2.8 | 2.9 | 3.2 | 2.9 | 3.1 | 3.4 | 3.3 | 3.4 | 3.5 |
| B户型 | 3.6 | 3.7 | 3.7 | 3.9 | 3.8. | 3.9 | 4.2 | 4.1 | 4.1 | 4.2 | 4.3 | 4.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{17}{8}$,+∞) | B. | (-∞,$\frac{17}{8}$] | C. | (-∞,2] | D. | [2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p或q | B. | (¬p)或(¬q) | C. | p且(¬q) | D. | p且q |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com