已知正数a1.a2.a3成等差数列.且其和为12,又a2.a3.a4成等比数列.其和为19.那么a4=( )A．12B．16C．9D．10 题目和参考答案——青夏教育精英家教网—

14．已知正数a₁，a₂，a₃成等差数列，且其和为12；又a₂，a₃，a₄成等比数列，其和为19，那么a₄=（　　）

A．

B．

C．

D．

分析由正数a₁，a₂，a₃成等差数列，且其和为12，求出a₂=4，又a₂，a₃，a₄成等比数列，其和为19，求出答案．

解答解：正数a₁，a₂，a₃成等差数列，且其和为12，
∴2a₂=a₁+a₃，a₁+a₂+a₃=12，
∴a₂=4，
∵又a₂，a₃，a₄成等比数列，其和为19，
∴a₃²=a₂a₄，a₂+a₃+a₄=19，
∴a₃=6，a₄=9，
故选：C．

点评此题考查学生掌握等差等比数列的性质，属于基础题．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：选择题

4．若函数f（x）=2^x+2^-x的定义域为R，则（　　）

	A．	f（x）为偶函数		B．	f（x）为奇函数
	C．	f（x）既奇又偶函数		D．	f（x）为非奇非偶函数

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

5．设集合M={0，2，-4，8}，N={x|x是4的倍数}，则M∩N=（　　）

A．

{2，-4}

B．

{0，2，-4}

C．

{0，-4，8}

D．

{-4，8}

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

2．若log_ab=c，则a，b，c之间满足（　　）

A．

a^c=b

B．

a^b=c

C．

c^a=b

D．

c^b=a

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

9．已知函数f（x）=lnx+ax²，g（x）=$\frac{1}{x}$+x+b，且直线y=-$\frac{1}{2}$是函数f（x）的一条切线．
（1）求a的值；
（2）对任意的x₁∈[1，$\sqrt{e}$]，都存在x₂∈[1，4]，使得f（x₁）=g（x₂），求b的取值范围
（3）已知方程f（x）=cx有两个根x₁，x₂（x₁＜x₂），若g（x₁+x₂）+2c=0，求证：b＜0．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

2．

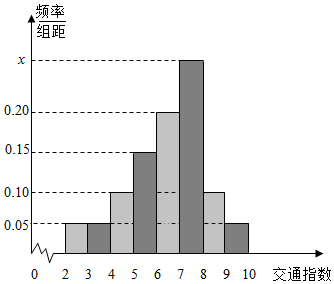交通指数是指交通拥堵指数或交通运行指数（Traffic Performance Index，即“TPI”），是反应道路畅通或拥堵的概念性数值，交通指数的取值范围为0～10，分为五级：0～2畅通，2～4为基本畅通，4～6轻度畅通，6～8为中度拥堵，8～10为严重拥堵．高峰时段，巴中市交通指挥中心随机选取了市区40个交通路段，依据交通指数数据绘制的频率分布直方图如图所示：
（Ⅰ）求出图中x的值，并计算这40个路段中为“中度拥堵”的有多少个？
（Ⅱ）在我市区的40个交通路段中用分层抽样的方法抽取容量为20的样本．从这个样本路段的“基本畅通”和“严重拥堵”路段中随机选出2个路段，求其中只有一个是“严重拥堵”路段的概率．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

9．$\int_0^2{（\sqrt{4-{x^2}}+x）dx}$=π+2．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

6．下列函数中，定义域为R且为增函数的是（　　）

A．

$y=-\frac{2}{x}$

B．

y=x³

C．

y=lnx

D．

y=tanx

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

7．

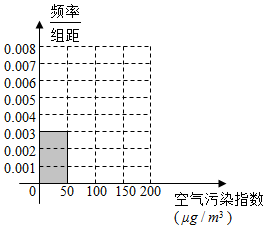空气污染，又称为大气污染，是指由于人类活动或自然过程引起某些物质进入大气中，呈现出足够的浓度，达到足够的时间，并因此危害了人体的舒适、健康和福利或环境的现象．空气污染指数与空气质量级别和空气质量状况的关系如下表：

空气污染指数单位：μg/m³	0～50	50～100	100～150	150～200	200～300	300以上
空气质量级别	一级	二级	三级	四级	五级	六级
空气质量状况	优	良	轻度污染	中度污染	重度污染	严重污染

2015年1月某日某省x个监测点数据统计如下：

空气污染指数（单位：μg/m³）	[0，50]	（50，100]	（100，150]	（150，200]
监测点个数	15	40	y	10

（Ⅰ）根据所给统计表和频率分布直方图中的信息求出x，y的值，并完成频率分布直方图；
（Ⅱ）若A市共有5个监测点，其中有3个监测点为轻度污染，2个监测点为良．从中任意选取2个监测点，事件A“其中至少有一个为良”发生的概率是多少？

查看答案和解析>>

同步练习册答案