
分析 由和的积分等于积分的和展开,然后由定积分的几何意义求得${∫}_{0}^{2}\sqrt{4-{x}^{2}}dx=π$,再求得${∫}_{0}^{2}xdx=\frac{1}{2}{x}^{2}{|}_{0}^{2}=2$,作和得答案.
解答 解:$\int_0^2{(\sqrt{4-{x^2}}+x)dx}$=${∫}_{0}^{2}\sqrt{4-{x}^{2}}dx{+∫}_{0}^{2}xdx$,
令y=$\sqrt{4-{x}^{2}}$,得x2+y2=4(y≥0),
则圆x2+y2=4的面积为4π,
由定积分的几何意义可得,${∫}_{0}^{2}\sqrt{4-{x}^{2}}dx=π$,
又${∫}_{0}^{2}xdx=\frac{1}{2}{x}^{2}{|}_{0}^{2}=2$,
∴$\int_0^2{(\sqrt{4-{x^2}}+x)dx}$=π+2.
故答案为:π+2.
点评 本题考查定积分,考查定积分的几何意义,考查微积分基本定理的应用,是基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 16 | C. | 9 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(0,\frac{6}{e^3})$ | B. | $(-3,\frac{6}{e^3})$ | C. | $(-2e,\frac{6}{e^3})$ | D. | (0,2e) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
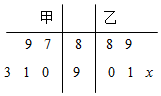 如图茎叶图记录了甲、乙两位射箭运动员的5次比赛成绩(单位:环),若两位运动员平均成绩相同,则成绩较为稳定(方差较小)的那位运动员成绩的方差为2.
如图茎叶图记录了甲、乙两位射箭运动员的5次比赛成绩(单位:环),若两位运动员平均成绩相同,则成绩较为稳定(方差较小)的那位运动员成绩的方差为2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{12}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com