
分析 由题意画出三棱锥的图形,取BC,AD的中点分别为E,F,求出AED的面积,然后求出棱锥的体积,再由导数确定函数的单调减区间.
解答 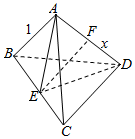 解:如图,四面体ABCD中,AD=x,其余各棱为1.取AD中点F,BC中点E
解:如图,四面体ABCD中,AD=x,其余各棱为1.取AD中点F,BC中点E
在三角形ABC中,∵三角形ABC为正三角形,E点是BC的中点,
∴AE⊥BC,同理ED⊥BC,
∵AE∩ED=E,∴BC⊥面AED.
S△AED=$\frac{1}{2}$AD•EF,
EF=$\sqrt{(\frac{\sqrt{3}}{2})^{2}-(\frac{x}{2})^{2}}$=$\frac{1}{2}\sqrt{3-{x}^{2}}$,
∴V(x)=$\frac{1}{3}$•S△AED•BC=$\frac{1}{3}•\frac{1}{2}x•\frac{1}{2}\sqrt{3-{x}^{2}}=\frac{1}{12}x\sqrt{3-{x}^{2}}$,
由3-x2>0,得0$<x<\sqrt{3}$,
∴函数V(x)的定义域为(0,$\sqrt{3}$),
V′(x)=$\frac{1}{12}\sqrt{3-{x}^{2}}+\frac{1}{12}x•\frac{1}{2}\frac{1}{\sqrt{3-{x}^{2}}}(-2x)$
=$\frac{1}{12}\sqrt{3-{x}^{2}}-\frac{1}{12}\frac{{x}^{2}}{\sqrt{3-{x}^{2}}}$=$\frac{1}{12}•\frac{3-2{x}^{2}}{\sqrt{3-{x}^{2}}}$,
由3-2x2<0,得x$<-\frac{\sqrt{6}}{2}$(舍),或x$>\frac{\sqrt{6}}{2}$.
∴函数V(x)的单调递减区间是($\frac{\sqrt{6}}{2},\sqrt{3}$).
故答案为:($\frac{\sqrt{6}}{2},\sqrt{3}$).
点评 本题考查棱锥的体积,考查空间想象能力,计算能力,关键是把棱锥转化为两个棱锥,考查利用导数一句话是的单调性,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5π}{6}$ | B. | $\frac{π}{6}$ | C. | $\frac{2π}{3}$ | D. | $\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
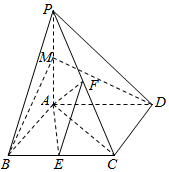 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,直线PC与底面ABCD所成的角45°,E,F,M分别是BC,PC,PA的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,直线PC与底面ABCD所成的角45°,E,F,M分别是BC,PC,PA的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com