
| A. | $\frac{5π}{6}$ | B. | $\frac{π}{6}$ | C. | $\frac{2π}{3}$ | D. | $\frac{π}{3}$ |
分析 对$\left|{\overrightarrow a+\overrightarrow b}\right|=\left|{\overrightarrow a-\overrightarrow b}\right|=\frac{{2\sqrt{3}}}{3}\left|{\overrightarrow a}\right|$平方得出$\overrightarrow{a}•\overrightarrow{b}=0$,${\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}$=$\frac{4}{3}{\overrightarrow{a}}^{2}$.从而得到${\overrightarrow{b}}^{2}$=$\frac{1}{3}{\overrightarrow{a}}^{2}$.计算($\overrightarrow{a}+\overrightarrow{b}$)•($\overrightarrow{a}-\overrightarrow{b}$)=${\overrightarrow{a}}^{2}-{\overrightarrow{b}}^{2}$=$\frac{2}{3}{\overrightarrow{a}}^{2}$.代入向量的夹角公式计算夹角的余弦.
解答 解:∵$\left|{\overrightarrow a+\overrightarrow b}\right|=\left|{\overrightarrow a-\overrightarrow b}\right|=\frac{{2\sqrt{3}}}{3}\left|{\overrightarrow a}\right|$,
∴$\overrightarrow{a}•\overrightarrow{b}=0$,${\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}$=$\frac{4}{3}{\overrightarrow{a}}^{2}$.
∴${\overrightarrow{b}}^{2}$=$\frac{1}{3}{\overrightarrow{a}}^{2}$.
∴($\overrightarrow{a}+\overrightarrow{b}$)•($\overrightarrow{a}-\overrightarrow{b}$)=${\overrightarrow{a}}^{2}-{\overrightarrow{b}}^{2}$=$\frac{2}{3}{\overrightarrow{a}}^{2}$.
∴cos<$\overrightarrow{a}+\overrightarrow{b},\overrightarrow{a}-\overrightarrow{b}$>=$\frac{\frac{2}{3}|\overrightarrow{a}{|}^{2}}{\frac{4}{3}|\overrightarrow{a}{|}^{2}}=\frac{1}{2}$.
∴<$\overrightarrow{a}+\overrightarrow{b},\overrightarrow{a}-\overrightarrow{b}$>=$\frac{π}{3}$.
故选:D.
点评 本题考查了平面向量的数量积运算,夹角计算,属于中档题.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
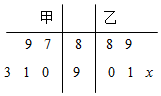 如图茎叶图记录了甲、乙两位射箭运动员的5次比赛成绩(单位:环),若两位运动员平均成绩相同,则成绩较为稳定(方差较小)的那位运动员成绩的方差为2.
如图茎叶图记录了甲、乙两位射箭运动员的5次比赛成绩(单位:环),若两位运动员平均成绩相同,则成绩较为稳定(方差较小)的那位运动员成绩的方差为2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1)∪(2,+∞) | B. | (0,+∞) | C. | (2,+∞) | D. | (-∞,0)∪(2,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com